das ist keine "Art Pythagoras" sondern der Pythagoras höchstpersönlich :-)
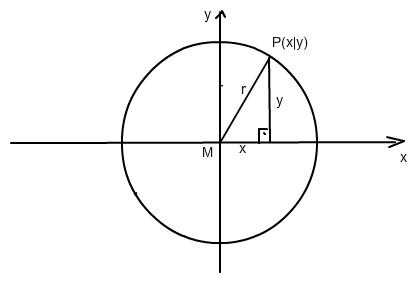
Für jeden Punkt (x|y) auf der Kreislinie gilt x2 + y2 = r2 (Pythagoras)
→ y2 = r2 - x2 → y = ± √( r2 - x2 )
y = √( r2 - x2 ) gilt für den oberen, y = - √( r2 - x2 ) für den unteren Halbkreis.
Gruß Wolfgang