Ein Reiseunternehmen plant eine kombinierte Bahn-Schiffsreise, die mindestens 200 Stunden dauern
soll. Der Reisepreis soll aus Vertriebsgründen einen Betrag von 900 EUR nicht übersteigen.
Es wird mit folgenden mittleren Reisegeschwindigkeiten bzw. Fahrpreisen kalkuliert:
Bahn: Geschwindigkeit: 60 km/h, Fahrpreis: 0,12 EUR/km
Schiff: Geschwindigkeit: 10 km/h, Fahrpreis: 0,18 EUR/km
x : Zeit bahn
y : Zeit schiff
x + y ≥ 200
x * 60 * 0.12 + y * 10 * 0.18 ≤ 900
Ziel : Strecke
x * 60 + y * 10 = max
y ≥ 200 -x
y * 10 * 0.18 ≤ 900 - x * 60 * 0.12
y ≤ ( 900 - x * 60 * 0.12 ) / 1.8
y ≤ 500 - 4x
Zeichnen
y ≥ 200 -x
y ≤ 500 - 4x
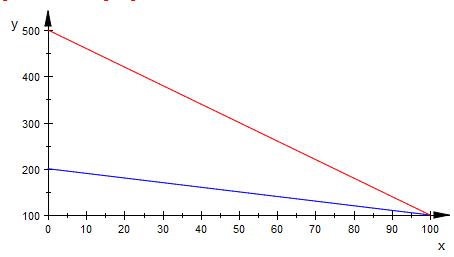 Eckpunkte
Eckpunkte
( 0 | 500 )
( 0 | 200 )
( 100 | 100 )
Zielfunktion
x * 60 + y * 10 = max
0 * 60 + 500 * 10 = 5000
0 * 60 + 200 * 10 = 2000
100 * 60 + 100 * 10 = 7000
Überprüfung der Ausgangsdaten
x + y ≥ 200
100 + 100 = 200
x * 60 * 0.12 + y * 10 * 0.18 ≤ 900
100 * 60 * 0.12 + 100 * 10 * 0.18 = 720 + 180 = 900
Bei Bedarf nachfragen.
Das mit der Restriktionsgeraden habe ich nicht
gemacht. Das Ganze nennt sich " Simplexverfahren ".