Volumen und Mantelfläche berechnen

Question

Aufgabe:

Volumen und Mantelfläche berechnen im Intervall (0,1) um X-Achse
x² + y² = 1

folgendes Problem:

Ich begreife nicht ganz, was ich genau einsetzen soll in die Formel für die Volumenberechnung um die x-Achse.

 

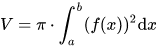
Soll ich nun x ² +y ² = 1 etwa quadrieren und dann Integration bilden?

Answer 1

Du musst erstmal eine Funktion machen

x^2 + y^2 = 1

y^2 = 1 - x^2

y = √(1 - x^2)

f(x) = √(1 - x^2)

(f(x))^2 = 1 - x^2

Comments

Hey @Der_Mathecoach, jetzt ergibt das ganze auch einen Sinn für mich. Eine Frage noch bezüglich des Umstellens. Hast du in dem Fall bewusst nach y umgestellt, weil wir das Volumen um die x-Achse haben wollen? Die 1-x^2 wurden doch bereits quadriert und müssen nur noch integriert werden, stimmts ? Schon mal großes Dankeschön für deine Hilfe

---

Genau. Diese obige Kreisberandung rotiert jetzt um die x-Achse und ergibt eine Kugel.