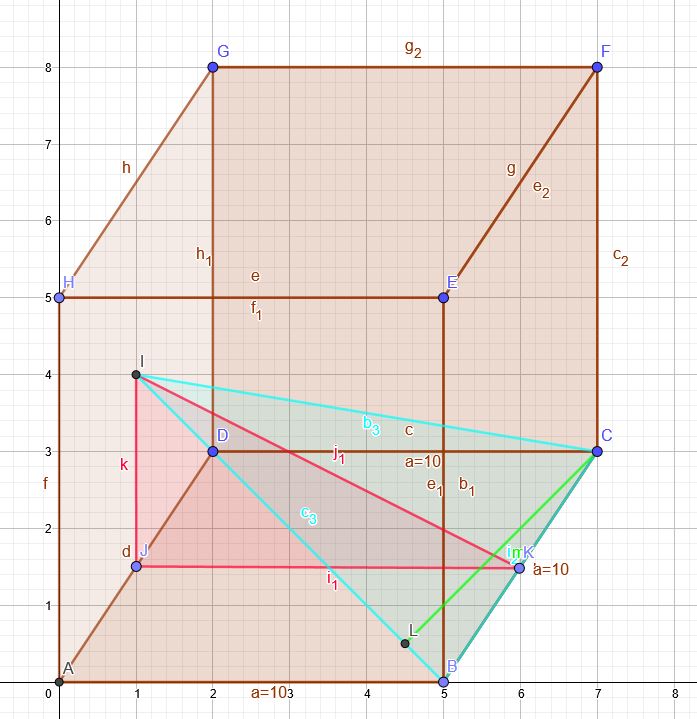
Vorderansicht des Würfels ist ABEH
Hinteransicht des Würfels ist DCFG
1.)
(J und K sind die jeweiligen Mitten der Kanten des Würfels)
Berechnung der Strecke I K ( rotes Dreieck) mit dem Satz des Pythagoras:
\(I K= \sqrt{(JK)^2+(IJ)^2} \) ( I ist der Diagonalenschnittpunkt der linken Seitenfläche ADGH des Würfels.)
\(I K= \sqrt{(10)^2+(\frac{10}{2})^2}= \sqrt{125}=5\sqrt{5} \)
2. ) Berechnung des Winkels BIC des blauen gleichschenkligen Dreiecks:
\(\tan(BIK)= \frac{BK}{IK}=\frac{5}{5\sqrt{5}}=\frac{1}{\sqrt{5}}=\frac{1}{5}\sqrt{5} \)
Der halbe Winkel von BIC ist nun \(\tan^{-1} (\frac{1}{5}\sqrt{5})=24,09°\)
Somit ist der ganze Winkel bei I \(48,18°\)
Der Winkel CBL hat eine Größe von\( \frac{180°-48,18°}{2}=65,91° \)
3.)Länge der Strecke CL (grün): \(\sin(65,91°)= \frac{CL}{10} \)
\(CL≈9,129\)