Kuckuck! :-)
Die Allgemeine Polynomfunktion 3. Grades und ihre ersten zwei Ableitungen sind:
f(x) = ax^3 + bx^2 + cx + d
f'(x) = 3ax^2 + 2bx + c
f''(x) = 6ax + 2b
Für das Entnehmen der Bedingungen aus dem Aufgabentext und für's Aufstellen der Gleichungen könnte eventuell eine Skizze helfen:

a)
Gesucht sind die Koeffizienten a, b, c, d.
Um sie berechnen zu können, brauchen wir 4 Gleichungen.
Aus dem Aufgabentext entnehmen wir die Bedingungen
"...(Koordinatenursprung ist im linken Endpunkt..."
f(0) = 0
"Dadurch senkt sich das Ende um 10cm."
f(5) = -0,1
"..deren Graph im linken Ende einen Hochpunkt hat..."
f'(0) = 0
"...im rechten Ende einen Wendepunkt."
f''(5) = 0
Jetzt können wir die Gleichungen aufschreiben.
f(0) = 0
a·0^3 + b·0^2 + c·0 + d = 0 I
⇒ d = 0
f(5) = -0,1
a·5^3 + b·5^2 + c·5 + 0 = -0,1
125a + 25b + 5c = -0,1 II
f'(0) = 0
3a·0^2 + 2b·0 + c = 0 III
⇒ c = 0
f''(5) = 0
6a·x + 2b = 0
6a·5 + 2b = 0
30a + 2b = 0 IV
Gleichung I liefert uns d = 0 und aus Gleichung III bekommen wir c = 0.
Wegen c = 0 wird aus Gleichung II
125a + 25b = -0,1
Da wir c und d bereits kennen bleiben uns die Unbekannten a und b, die wir mit Hilfe
der Gleichungen II und IV berechnen können, indem wir das lineare Gleichungssystem
125a + 25b = -0,1
30a + 2b = 0
lösen. Wir lösen das Mini-LGS und bekommen
a = 0,0004
b = -0,006
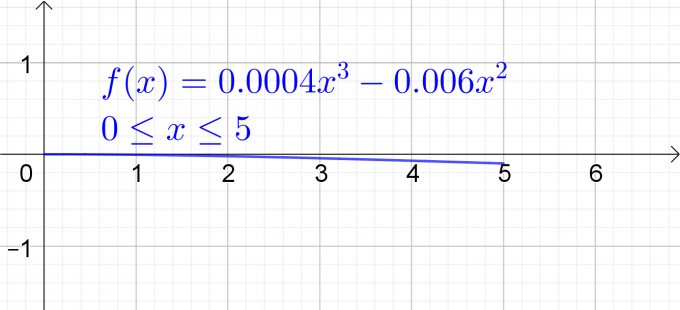
Die gesuchte Polynomfunktion ist f(x) = 0,0004x^3 + -0,006x^2
b) f'(5) = ?
:-)
Beste Grüße