Pyramidenhöhe mit Vektoren berechnen

Question

 

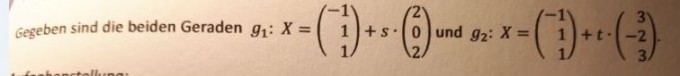
Aufgabenstellung:

1) Begründen Sie die Behauptung, dass sich beide Geraden in einem Punkt A schneiden und einen rechten Winkel einschließen, indem Sie die Koordinaten des Schnittpunktes abgeben und die Rechtwinkeligkeit der beiden Geraden rechnerisch nachweisen

2) Bestimmung der Koordinaten zweiter Punkte: B und D, mit B auf g1 und D auf g2, die vom Schnittpunkt A der beiden Geraden 5cm entfernt sind

3) Mittelpunkt der Strecke BD ermitteln

4) Ermitteln der Parameterdarstellung jener Geraden, die normal auf die durch die Geraden g1 und g2 bestimmte Ebene steht und durch den Punkt M geht.

danke und lg

Comments

Vom Duplikat:

Titel: Pyramidenhöhe mithilfe von Vektoren berechnen

Stichworte: vektoren,pyramide,textaufgabe

null plan. bitte um eure hilfe. danke

 

Answer 1

a)
Beide Geraden haben A = [-1, 1, 1] als Stützvektor (Ortsvektor). Dieses ist daher der Schnittpunkt der Geraden.

Das Skalarprodukt der Richtungsvektoren ist [2, 0, 2] * [3, -2, 3] = 6. Da das Skalarprodukt nicht 0 ist stehen die Geraden NICHT rechtwinklig zueinander.

Prüfe mal ob die Geraden wirklich zu der Aufgabe gehören.

Comments

ja gehören zur aufgabe. das problem ist ja auch, dass unser lehrer gerne fehler macht. oft schreibt er falsch ab, zb.

nja, wird wohl so ein fehler sein. trotzdem danke.

---

Das kenne ich. Ich verstehe auch nicht warum die Lehrer immer meinen selber Aufgaben stellen zu müssen die vorne und hinten nicht stimmen. Dann sollen sie lieber Aufgaben aus dem Buch aufgeben.

---

ja stimmt, denn für das buch haben wir lösungen... :(
trotzdem danke für eure unterstützung :)