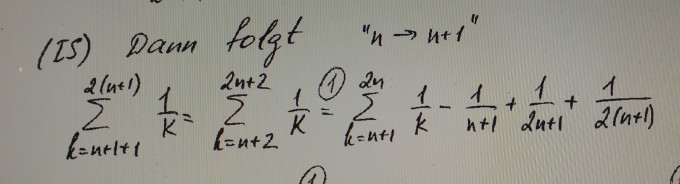ich habe eine Frage wie ich den Index bei vollständiger Induktion handhaben muss.
In diesem Beispiel habe ich vorher oben 2n und unten k = n+1, dann rechne ich n+1, das ist mir bis dahin klar. Nur dann habe ich oben 2n+2 und unten k = n+2. Was muss ich jetzt rechnen damit ich auf die Gleichung rechts komme, sodass im Index des Summenzeichens wieder 2n oben und k = n+1 unten steht? Vielen Dank