pa1(x) = a1 * x^2 +(1+a1) * x + 1
pa2(x) = a2 * x^2 +(1+a2) * x + 1
a1 * x^2 +(1+a1) * x + 1 = a2 * x^2 +(1+a2) * x + 1
a1 * x^2 +(1+a1) * x = a2 * x^2 +(1+a2) * x
x * ( a1 * x +(1+a1)) = x * ( a2 * x +(1+a2) )
x = 0
( Wenn man will kann man hier schon aufhören.
Der Nachweis ist erbracht.
a1 * x +(1+a1) = a2 * x +(1+a2)
a1 * x +1 +a1 = a2 * x +1+a2
a1 * x +a1 = a2 * x +a2
a1 * ( x + 1 ) = a2 * ( x + 1 )
x + 1 = 0
x = -1
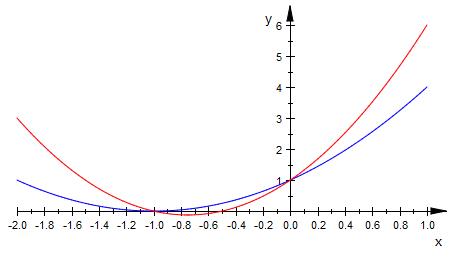
Alle Scharfunktionen schneiden sich in
x = 0 und x = -1
Hier ein Beispiel