bei folgender Aufgabe komme ich immer auf ein anderes Ergebnis als im Lösungsheft:
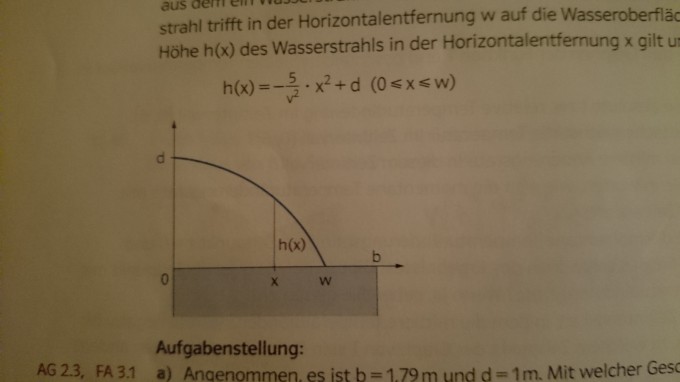
Für die Höhe des Wasserstrahls in der Horizontalentfernung gilt: h(x)=(-5x^2)/v^2+d
1) x=1,8 m [EDIT: Korrigiert gemäss Kommentar]
v=3m/s
a) welchen Winkel bildet der Wasserstrahl mit der horizontalen Wasseroberfläche, wenn er gerade die halbe Horizontalentfernung x zurückgelegt hat?
b) Wie groß ist dieser Winkel beim Aufprall?
Für a sollte laut Lösungsheft 45Grad und für b 63,43 Grad rausbekommen... Ich erhalte die beiden Werte immer umgekehrt...
Kann ma mal bitte jemand nachrechnen?
LG
EDIT: Nochmals Änderung gemäss Kommentar (nachgereichtes Bild):