tut mir leid, ich konnte nicht einschätzen, dass diese frage aufgabenspezifisch ist, dachte ist eine normale umformung...
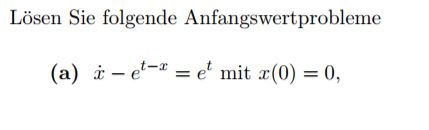
Das ist das ende der Lösung.. habe ich auch damals aus Mathelounge...
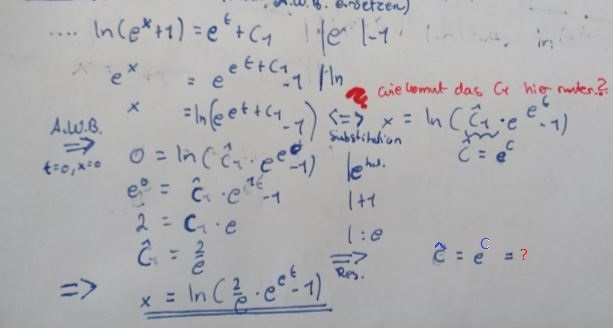
also könnte es vielleicht sein, dass C= ln(2/e) ist? => x= ln(e^ln(2/e)...) und das ln und e heben sich auf und bleibt 2/e übrig?
mfg