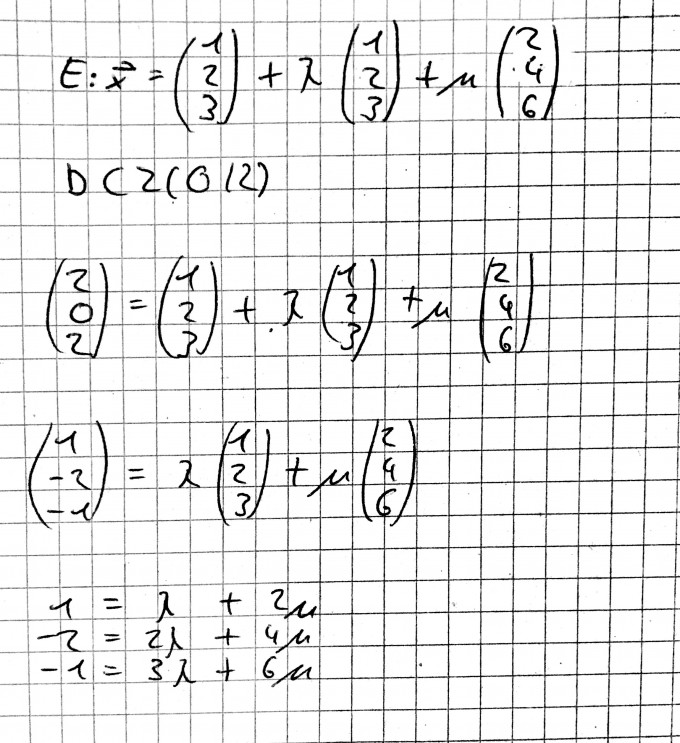Liegen die Punkte A,B, C und D in einer gemeinsamen Ebene?

Question

ich soll überprüfen ob, die Punkte A,B, C und D in einer gemeinsamen Ebene. A(1/2/3), B(2/4/6), C(3/6/9), D(2/0/2) Ich habe jedoch das Problem, dass beim lambda bzw. mü ausrechen, es stets 0 wird. z.B. wenn ich die obere Zeile in die Zweite einsetze: 1 - 2µ = λ dann bekomme ich -2= 2 + 0µ.   -4=0µ kann doch nicht richtig sein, oder?

Comments

Du machst bereits einen Fehler, wenn du AB und AC als Richtungsvektoren nimmst weil diese Linear abhängig sind und nur eine Gerade aufspannen. Damit erreichst du nur Punkte die auf einer Geraden liegen.

Answer 1

A(1/2/3), B(2/4/6), C(3/6/9), D(2/0/2)

AB = [1, 2, 3]

AC = [2, 4, 6]

AD = [1, -2, -1]

Da AB linear abhängig zu AC liegen A, B und C auf einer Geraden. Da AD nicht linear abhängig zu AB liegen die 4 Punkte in einer Ebene.

Comments

Also für die Ebenengleichung dürfen die Spannvektoren nicht linear abhängig bzw. das Vielfache vom Anderen sein, korrekt?

---

Richtig. Sonst spannst du nur eine Gerade auf. Dazu langt dann aber auch nur ein Vektor.