Funktion aus einem Graphen bauen?

Question

angenommen ich habe eine Form (bzw. einen Graphen welcher z.B aussieht wie der Umriss eines Autos) mit eindeutigen x- und y Koordinaten, wie lässt sich die dazugehörige Funktion (wenn überhaupt eine gibt) ermitteln oder selbst "bauen"? Anbei mal ein "gemalter" Graph damit man weiß worauf ich hinaus will..  

Answer 1

" Eine Funktion " wirst du wahrscheinlich nicht
herausbekommen.
In der Praxis teilt man die Funktion in
mehrere Abschnitte auf die dann jeweils z.B.
als Polynom 2.Grades mit 3 Stützstellen
berechnet werden.

Comments

Hallo Georg,

gibt es da eventuell ein Beispiel aus der Praxis? Also die Vorgehensweise? (vielleicht im Netz)

---

Du liest 3 Stützstellen aus dem Graphen ab
z.B.
( 0 | 0 )
( 1 | 1 )
( 3 | 2 )

und berechnest daraus eine Funktion 2.Grades.
f ( x ) = a * x^2 + b * x + c
f ( x ) = -x^2 / 6 + 7/6 * x

Dann läßt du dir die Funktion im Intervall
0..3 plotten und vergleichst den Graph
mit dem Plot ob eine zufriedenstellende
Übereinstimmung vorhanden ist.

Ein " Schema f " für alle Graphen gibt
es nicht.

Answer 2

Schau mal dort:

https://de.wikipedia.org/wiki/Interpolation_(Mathematik)#Einführung

speziell für die Formen von Autos empfiehlt sich 

https://de.wikipedia.org/wiki/Bézierkurve

Answer 3

Zwar hast Du die "beste Antwort" schon vergeben, aber wenn ich lese

"Eine Funktion wirst Du ... nicht herausbekommen..."

möchte ich einige Lösungswege vorstellen, die beliebig verfeinert werden können.

§1: Polynominterpolation

Unter http://www.gerdlamprecht.de/Mittelwerte.html kann man z.B. n Stützstellen eingeben und bekommt ein Polynom (n-1). Grades heraus.

13 Stützstellen:
y[]: 0,0.3,0.6,1.8,2.2,2.2,2.8,3.3,3.3,2.5,2,1.6,0
x[]: 0,0.5,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,... ergibt
x*27720759/70449601+pow(x,2)*167388058/84742151-pow(x,3)*123900741/20833861+pow(x,4)*161981647/20649973-pow(x,5)*337341829/63183357+pow(x,6)*167637325/78742134-pow(x,7)*13720140/25689827+pow(x,8)*7597756/87301631-pow(x,9)*300047/32554700+pow(x,10)*6969/11375647-pow(x,11)*17/731908+pow(x,12)/2609339

mit pow(x,y)=x^y

Da es zu wenig Stützstellen sind und das Polynom ein recht hohen Grad hat, gibt es zwischen den Stützstellen recht hohes Überschwingen. 

Die Funktion ist gleich kompatibel zum Plotter unter

http://www.gerdlamprecht.de/Liniendiagramm_Scientific_plotter.htm ergibt das Bild

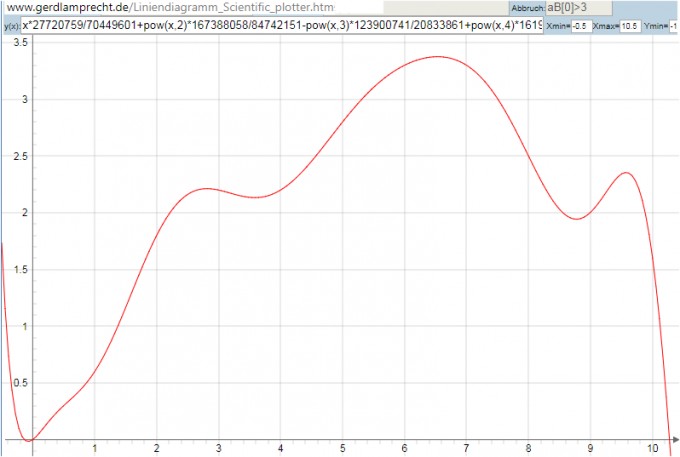
Wem nun das Autodach zu rund ist, kann diesen Abschnitt anpassen:

§2: abschnittsweise Anpassung
a) hart: (x>5.7&&x<7.2)?3.2: was auch leicht mit anderen expliziten Funktionen wie exp(-x*x)=e^{-x²}*Faktor+Restfunktion für andere Plotter kompatibel gemacht werden kann

 
(x>5.7&&x<7.2)?3.2:x*27720759/70449601+pow(x,2)*167388058/84742151-pow(x,3)*123900741/20833861+pow(x,4)*161981647/20649973-pow(x,5)*337341829/63183357+pow(x,6)*167637325/78742134-pow(x,7)*13720140/25689827+pow(x,8)*7597756/87301631-pow(x,9)*300047/32554700+pow(x,10)*6969/11375647-pow(x,11)*17/731908+pow(x,12)/2609339 ergibt:

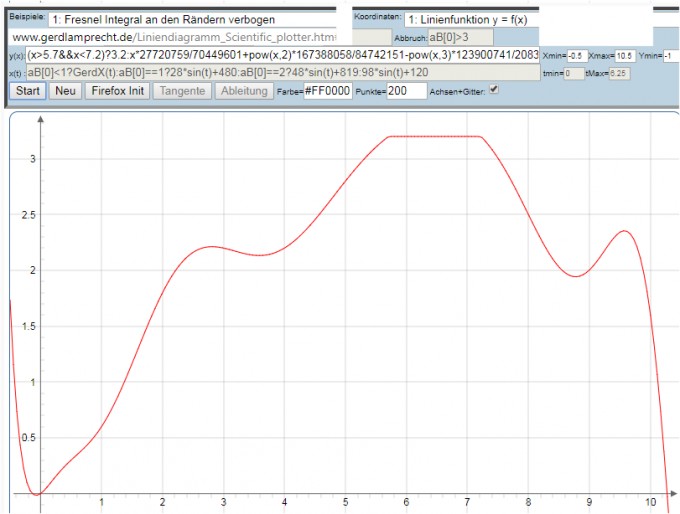
b) weich: kubische Splines oder andere höhere Funktionen

Der Plotter zeigt z.B. im Beispiel 83, dass selbst die Silhouette einer Frau kein Problem ist!

Siehe auch Beispiel 98 Batman-Kurve

Statt abschnittsweiser Anpassung von Bereichen, kann man auch die 

§3: trigonometrische Interpolation
mit beliebig viele Stützstellen heranziehen.

f(x)= a*sin(b*x+c)+d*sin(... + ...

Der Plotter zeigt im Beispiel 105 die Bitcoin-Formel/Kurve

und zig andere Beispiele 118 Schreibschrift

Beispiele von Nikolaus-Haus über Depeche Mode Formel bis hin zu Gesichtern

http://www.gerdlamprecht.de/Beispielbilder_zum_Universal_Diagramm_Plotter.html

Da das handgezeichnete Bild keine besondere Qualität hat, stecke ich jetzt nicht viel Zeit in eine Beispielformel rein. Für richtig gute Quell-Bilder habe ich ein Vektorisierungsprogramm, 

welches SVG-Bilder erzeugt. Aus diesen Vektor-Kurven lässt sich dann per PC eine schöne lange explizite Funktion basteln. Catherine Zeta-Jones Formel hatte über 99000 Zeichen.

Das funktioniert auch in 3D wie im Beispiel 23 unter

http://www.gerdlamprecht.de/3D-online-Plotter.htm