Das Fazinierende bei dieser Art Aufgaben ist doch, dass obwohl Grosserloewe ursprünglich einen Fehler gemacht hat ..
$$1-4x \colorbox{#FF0}{+}2\sqrt{1-4x} +1= -2x$$
... trotzdem das richtige heraus kommt, weil eben zwischendurch wieder quadriert wird womit das Vorzeichen obsolet ist. Würde die Ausgangsgleichung so lauten:
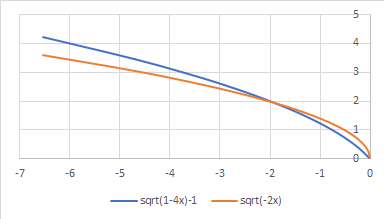
$$\sqrt{1-4x} + 1 = \sqrt{-2x}$$
wäre die Rechnung zwar identisch und auch korrekt, aber bei der Probe zeigt sich dann, dass keiner der berechneten Werte eine Lösung ist. Es lohnt also immer ein kleines Diagramm