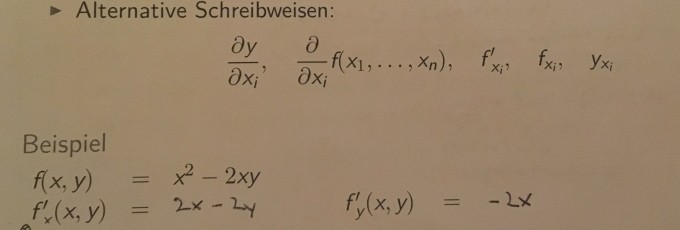Partielles Ableiten: Grundlagen - Wieso ist f(x,y) = x^2 - 2xy nach y abgeleitet -2x?

Question

Ich lese mich gerade frisch in das Thema ein. Eine Funktion mit mehreren Variablen partiell nach einer Variable x ableiten, bedeutet doch, alle Produkte in denen x vorkommt, ableiten und alle anderen Produkte unbeachtet lassen oder?

Beim ersten Fall nach x ist das der Fall, beim zweiten Fall nach y hätte ich abgeleitet x^2 - 2x gebildet.

 

Answer 1

so ungefähr ist das. 

Noch ein Beispiel:

$$f(x,y)=x^2+y^2-3x+y\\{f´}_{x}(x,y)=2x+y^2-3+y\\{f´}_{y}(x,y)=x^2+2y-3x+1$$

Ich hoffe, das ist verständlich.

Smitty

Comments

Danke dir. Also ist mein Aufschrieb auf dem Foto falsch?

PS: Wieso hast du in der letzten Gleichung 3y und nicht 3x stehen?

---

Dein Aufschrieb ist richtig. Ich habe nur ein anderes Beispiel gewählt.Das mit dem y war ein Tippfehler, soll x heißen => wird verbessert. 

EDIT: nach y ist bei dir Falsch: die Ableitung ist: x^2-2x

---

Meinst du mit meinem Aufschrieb die Beschreibung der Frage, oder die Version auf dem Foto?

---

Sorry für meinen Denkfehler. Nach x ist in deinem Beispiel richtig. Aber die Ableitung nach y ist nicht richtig. s.o.

---

Danke für die Bestätigung!

---

Auf den nächsten Seiten habe ich dies allerdings wieder “falsch” abgeschrieben. Ich bin unsicher:

  

---

Warte dein Aufschrieb ist doch richtig, ich hatte irgendwie die Regeln gemischt...

Sorry..

Da x^2 ein Summand ist, wird x als Konstante gesehen. In einem Produkt bleibt der Faktor erhalten.

Bei meinem Beispiel:

f(x,y)=x^2+y^2-3x+y

f´_x(x,y)= -2x-3

f´_y(x,y)= 2y+1

---

Auf der Seite ist es gut erklärt. https://www.mathebibel.de/partielle-ableitung

Ich bitte um Verzeihung für meine Fehler.

---

Kein Problem. Also die Summanden mit der abzuleitenden Variable werden abgeleitet, die anderen Variablen werden zu null.