Zeigen Sie, dass die folgende Abbildung total diffbar ist und bestimmen Sie die Jacobimatrix. Verknüpfung von f und g.

Question

es geht um die folgende Aufgaben:

a und b habe ich fertig. die sind total diffbar:

c ist auch total diffbar, da sie die Komposition zweier total diffbarer Abbildungen ist... 

und mein Ansatz ist folgendes:

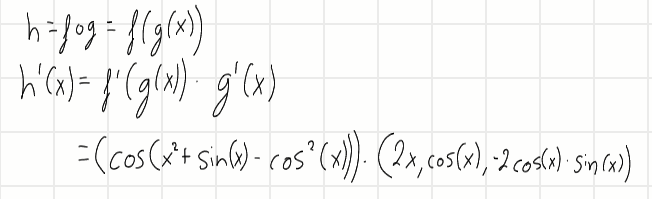
Wir nehmen nur den X-Anteil von f, da g ja auch nur x besitzt... 

Aber das Ergebnis stimmt aus irgendeinem Grund nicht? der Vektor rechts ist falsch. In der Lösung ist folgendes:

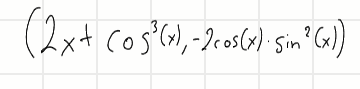
Wie kommt man hier drauf?... mit meiner Variante stimmen die Dimensionen ja nicht überein also muss man das umwandeln... 

mfg

Comments

oh da sollte kein , am Ende sein... hier das richtige:

Answer 1

Du solltest Dich entscheiden, ob Du für die Jacobi-Matrix \(f'\) oder \(J_f\) schreiben willst, und dann dabei bleiben. Jedenfalls ist dein \(J_f\) nicht richtig hingeschrieben, denn das ist ein Zeilenvektor bzw. eine \(1\times3\)-Matrix. \(J_f\) ist ok, denn das ist ein Spaltenvektor bzw. eine \(3\times1\)-Matrix. Und nach der Kettenregel ist dann \(J_h(x)=J_f(g(x))J_g(x)=J_f(x^2,\sin x,\cos^2x)J_g(x)\). Das ist jetzt nur noch einsetzen und ausrechnen. DIe Bemerkung "Wir nehmen nur den X-Anteil von f, da g ja auch nur x besitzt... " ist voellig daneben!

Comments

also da steht \(f \circ g\) also nehme ich g' ... aber nun weiß ich nicht was ich für f' nehme? ich habe die x-Komponente von J_f genommen und da mein g(x) eingesetzt, wie eben die Definition einer Komposition ist... du meinst ich sollte J_f (x,y,z) nehmen und da g(x) in x,y und z einsetzen?... o.O das wir jetzt eine lange rechnung aber ich probiers mal... 

---

ich soll also das hier lösen? 

mfg

---

So das war leichter als gedacht... 

\(= 2x*cos(x^2+sin(x)*cos^2(x))+cos^2(x)(x^2+sin(x)*cos^2(x))*cos^2(x)-2cos^2(x^2+sin(x)*cos^2(x))sin^2(x)

=(2x+cos^3(x)-2cos^2(x)*sin^2(x))*cos(x^2+sin(x)*cos^2(x))\)

danke! :D

---

\(f'\) ist eine Zeile und \(g'\) ist eine Spalte, nicht umgekehrt.

Merkregel für Jacobi-Matrizen: Die Komponenten der Funktion untereinander, die Ableitungen von links nach rechts.