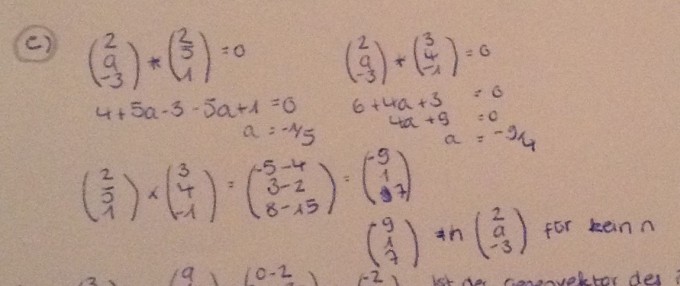Ich hab mehrere Wege gefunden die Aufgabe zu lösen? Aber sind das überhaupt Lösungswege und sind die korrekt? Die Schar wird beschrieben durch 2x1+ax3-3x3=1 und F durch (1/-2/3) + r(2/5/1) + s(3/4/-1)
Also hier mein Ansatz:
1. Den Normalenvektor von Ea also (2/a/-3) mit den beiden Richtungsvektoren von F skalarmultiplizieren. Das muss dann 0 ergeben für das gleiche a.
Ich habe da für a= -1/5 und a=-9/4, da das verschieden a's sind, habe ich schlussgefolgert, dass es keine Ebene von Ea gibt, die parallel zu F ist.
2. Kreuzprodukt der Richtungsvektoren von F, also Normalenvektor von F, der kollinear zum Normalenvektor von Ea sein muss.(-9/1/7)=n(2/a/-3) ist für kein n und a erfüllt.
Ist das so richtig?
Hier nochmal ausführlich die Bearbeitung der Aufgabe: