Hallo SomO,
im ersten Fall wird der 'Aufhängepunkt' der Gerade verschoben, wenn \(p_2 \ne 0\). Und zwar um den Vektor \((0|p_2)\) Und im zweiten Fall ändert sich gar nichts, da der Richtungsvektor nur mit einer Konstanten (hier der 2) multipliziert wird. Der Richtungsvektor gibt nur die Richtung der Geraden vor, seine Länge sagt nichts über die Gerade.
Ein Beispiel:
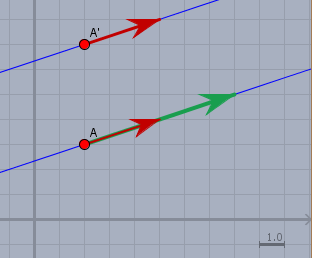
Die Gerade sei durch den Aufhängepunkt Punkt \(A=(2|3)\) und durch den roten Vektor \((3|1)\) gegeben. Im ersten Fall wird aus \(A\) \(A'=(2|2\cdot3)=(2|6)\). Die Gerade wird parallel nach oben verschoben. Im zweiten Fall wird nur der Richtungsvektor verdoppelt und zum grünen Vektor \((6|2)\). Die Gerade selbst beeinflusst das nicht.
Gruß Werner