Hallo Cecilia,
den Abstand zwischen zwei Punkten berechnet man mit
$$ d=\sqrt{(x_1-x_2)^2+(y_1-y_2)^2} $$
Gesucht wird der Punkt (x|f(x))
Seien x1 = 2, x2 = x, y1 = 3 und y2 = -x3+3x2
In die Formel eingesetzt ergibt das
$$ d=\sqrt{(2-x)^2+(3-(-x^3+3x^2))^2} $$
$$ d=\sqrt{(2-x)^2+(3+x^3-3x^2)^2} $$
Das ist die Zielfunktion.
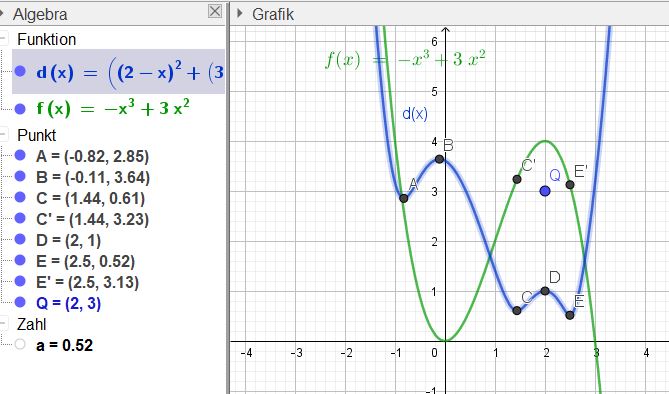
Um den kleinsten Abstand zu bestimmen, werden die Tiefpunkte der Funktion gesucht (f'(x) = 0)
Wie aus dem Schaubild ersichtlich, kommen nur die Punkte C und E als Minimumstellen in Frage. (Den Rechenweg spare ich mir an dieser Stelle)
Du setzt die Koordinaten der beiden Punkte C' und E' in die Gleichung d = ... ein und erhältst dann die Abstände für C' = 0,61 und E' = 0,52.
Also ist E' der Punkt auf K mit dem kleinsten Abstand zu Q.
Gruß, Silvia