Funktion und Definitionsmenge von f mit f(x)=-3x^2-12x- 17 und g mit g(x)= 1/(x+3). erklärung

Question

Aufgabe:

Gegeben sind die beiden Funktionen f mit f(x)=-3x^2-12x- 17 und g mit g(x)= 1/(x+3).

a) Bestimme die Definitionsmenge D(f) und D(g).

b) Bestimme die Funktionswete von f und g an den Stellen 9 und 0,25.

c) Skizziere die Graphen von f und g mithilfe einer Wertetabelle und notiere die Wertemenge W(f) und W(g).


Lösung:

a) D(f)=R D(g)= R/ (-3)

b) f(9) = -368
f(0,25) = -(323/16)
g(9) = 1/12
g(0,25) = 4/ 13

c) W(f) = )-unendlich;-5)
W(g)R/ (0)

Frage:

Wie komme ich auf die Lösungen (insbesondere Berechnungen)?

Answer 1

Hi,

 

a) Was darf x nicht sein ist hier die Frage. Bei f gibt es keine Problemstellen, bei g sehr wohl. Der Nenner darf nicht 0 werden und somit ist die Nennernullstelle im Definitionsbereich nicht enthalten.

 

b) Ersetze x durch die gewünschten Zahlen und rechne aus.

 

c)

Wenn Du die Wertetabelle für f zwischen -5 und 5 machst, wirst Du feststellen, dass der größte Wert bei x=-2 zu finden ist. Das ist also die Obergrenze des Wertebereichs.

 

Wir haben hier bei g eine sogenannte (einfache) "Polstelle". Das bedeutet, dass außer Ausnahmen alle Zahlen in ℝ erreicht werden können. Du wirst feststellen, dass g(x)=0 nicht zubestimmen ist -> gehört also nicht zur Wertemenge.

 

Um die Wertemenge zu beschreiben, ist es immer gut eine Wertetabelle zu haben...bzw. diese allein bringt im zweiten Fall eher weniger, aber ein Schaubild zu haben! ;)

 

Grüße

 

P.S.:

Schaubild für g(x)

 

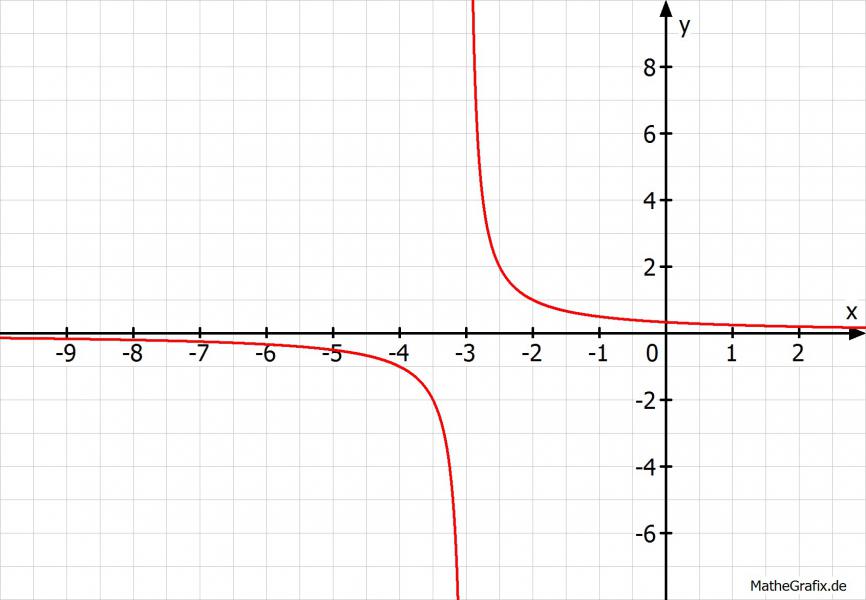
Übersetzung von "Wertebereich": "Was kann y alles sein".