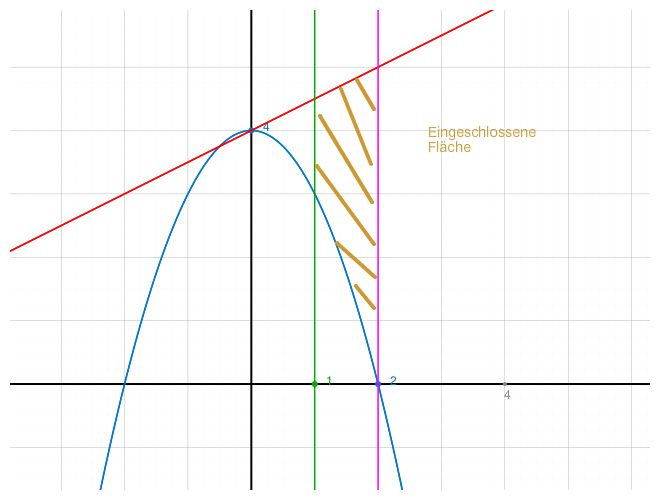
Hier mal die Rechnung und eine Skizze für 1.
f(x)= 4-x2 und g(x)= 1/2x+4 über dem Intervall [1;2]
d(x) = f(x) - g(x) = -x^2 - 0.5x
Stammfunktion davon
D(x) = -1/3 x^3 - 1/4 x^2
Fläche = | -1/3 *8 - 1/4 * 4 - (-1/3 - 1/4)| = |-8/3 - 1 + 1/3 + 1/4 | = 3.0833