Teil 1: https://www.mathelounge.de/529251/artikel-regression-berechnung-regressionskoeffizienten
Wie im vorangegangenen Teil bereits angekündigt, werden wir nun verifizieren, dass die aufwendig ermittelte Regressiongerade $$y=-0.8x+1.6=1.6-0.8x$$ für die Messwerte \(\{(x,y)\mid x,y\in\mathbb{R}\} :=\left\{(-2,4),(-1,2),(0,1),(1,0),(2,1)\right\}\) korrekt ist (nach der Methode der kleinsten Quadrate).
public static void main(final String... args){
// Datensatz vorbereiten
List<Data> data = new ArrayList<>();
data.add(new Data(-2,4));
data.add(new Data(-1,2));
data.add(new Data(0,1));
data.add(new Data(1,0));
data.add(new Data(2,1));
// Aufruf der Funktion zur Berechnung der linearen Ausgleichsgeraden.
regression(data);
}
Auf der Konsole wird korrekterweise $$ 1.6-0.8*x$$ ausgegeben. Dass dieses Ergebnis plausibel ist, können wir der graphischen Darstellung der Punkte und der Regressionsgeraden erkennen:
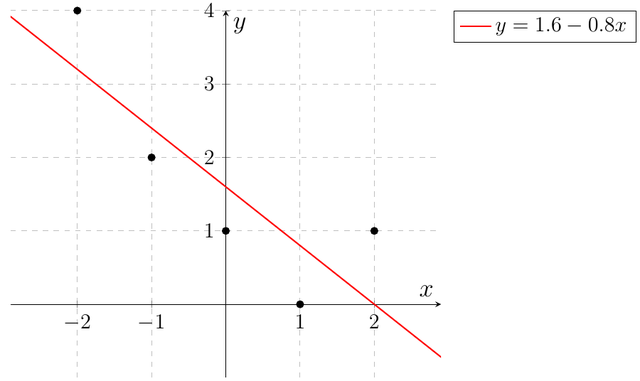
5. Beispiel für die direkte Ermittlung der Regressionsgeraden
Eine direkte Berechnung der Regressionskoeffizienten \(a_0\) und \(a_1\) ist dank der im dritten Abschnitt hergeleiteten Formel
- \(n=5\), da wir \(5\) Messwerte haben.
- \(\sum\limits_{k=1}^{n}{y_k}=4+2+1+0+1=8\)
- \(\sum\limits_{k=1}^{n}{x_k}=-2+(-1)+0+1+2=0\)
- \(\sum\limits_{k=1}^{n}{x^2_k}=(-2)^2+(-1)^2+0^2+1^2+2^2=4+1+0+1+2=10\)
- \(\sum\limits_{k=1}^{n}{x_k\cdot y_k}=(-2\cdot 4)+(-1\cdot 2)+(0\cdot 1)+(1\cdot 0)+(2\cdot 1)=-8+(-2)+0+0+2=-8\)
- \(\varphi = \dfrac{1}{n\cdot \sum\limits_{k=1}^{n}{x^2_k}-\left(\sum\limits_{k=1}^{n}{x_k}\right)^2}=\dfrac{1}{5\cdot 10-0^2}=\dfrac{1}{50}\)
- \(a_0=\dfrac{1}{50}\cdot \left(8\cdot 10-0\cdot (-8)\right)=\dfrac{80}{50}=1.6\)
- \(a_1=\dfrac{1}{50}\cdot \left(5\cdot (-8)-0\cdot 8\right)=\dfrac{-40}{50}=-0.8\)
ebenfalls möglich und erspart einem in der Prüfung wertvolle Denkzeit. Für unser Beispiel mit den Messwerten \(\{(x,y)\mid x,y\in\mathbb{R}\} :=\left\{(-2,4),(-1,2),(0,1),(1,0),(2,1)\right\}\) sieht das folgendermaßen aus:
Dieser Artikel hat 50 Bonuspunkte erhalten. Schreib auch du einen Artikel.