Hoch- und Tiefpunkte berechnen.

Question

Funktion lautet x^3 - 12x. Welche Nullstellen kommen raus?

Comments

Wie hängen deine Überschrift, Tags und Fragetext zusammen?

Achtung:

Ripper (und vielleicht auch frei2d2 ) lassen jeweils einen Teil der Fragestellung weg. Bsp. https://www.mathelounge.de/530953/hoch-und-tiefpunkte-funktion-lautet-f-x-1-8x-4-1-3x-3-1

und

https://www.mathelounge.de/531014/berechnung-der-hoch-und-tiefpunkte-f-x-x-3-3x-2

Answer 1

welche nullstellen kommen raus

$$ x_{1,2}=\pm2\sqrt{3}, x_{3}=0 $$

Comments

Eine nullstelle müsste null sein.

---

Danke, hab ich auf die Schnelle vergessen!

Answer 2

Hi,

f(x) = x^3-12x = 0

x(x^2-12) = 0

x_(1) = 0 und x_(2,3) = ±√12 = ±2√3

Alles klar?

Grüße

Answer 3

In der Überschrift suchst du nach Extrema.

f(x) = x³-12x. f '(x)=3x²-12; 0=3x²-12=3(x+2)(x-2). Extrema bei x=2 und bei x=- 2.

Answer 4

hier erstmal der Graph

~plot~ x^3-12x ~plot~
$$\text{lokale Extrempunkte}\\f(x)=x^3-12x\\f'(x)=3x^2-12\\f''(x)=6x\\\text{notw. Bed.}\\f'(x)=0\\3x^2-12=0\\x^2-4=0\\\text{erhalte mittels der pq-Formel}\\{x}_{1/2}=\pm2\\\text{hinr. Bed.}\\f'(x) = 0\text{ und }f''(x)\neq 0\\f''(2)=12>0=> Tiefpunkt\\f''(-2)=-12<0=> Hochpunkt$$

Jetzt musst du nur noch die y-Werte notieren.

Gruß

Smitty

(Übertragsfehler korrigiert. Unknown)

Comments

wieso setzt du nicht die erste Ableitung gleich null

---

6x² -12x = 0

Da hat Smitty sich vertippt, vgl. meine Antwort

---

Jo, da habe ich mich vertippt, kannst du das vielleicht editieren, Wolfgang?

Ich wäre dir sehr dankbar.

---

Das überschreitet leider meine Kompetenzen :-)

Aber Lu oder Unknown werden das wohl machen. Ich markiere deshalb deinen Kommentar.

---

Hoffentlich passend überarbeitet.

Grüße

---

Dankeschön :)

Gruß

Smitty

Answer 5

f(x) = x³ - 12·x  = x · (x² - 12) = 0

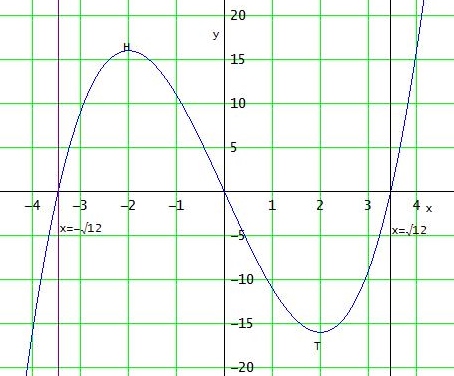
 ergibt nach dem Nullproduktsatz die Nullstellen  x₁ = 0   und x_2,3 = ±√12 

Hoch- und Tiefpunkt:

f '(x) = 3·x² - 12 = 0    ⇔  x = ± 2   (mögliche Extremstellen)

f "(x) = 6x  →  f "(2) = 12 > 0      →  T(2|-16)

                       f "(-2) = -12 < 0    →  H(-2|16)

Gruß Wolfgang

Comments

die erste Ableitung muss doch gleich null gesetzt werden

---

Ja, steht doch da:

f '(x) = 3·x² - 12 = 0    ⇔  x = ± 2

Das ergibt die möglichen Extremstellen.
Mit f(x) = 0  wurden zuerst die Nullstellen von f berechnet, also die x-Stellen, bei denen der Graph die x-Achse schneidet.