Hallo Sliverdart,
das entscheidende hier, ist die Tatsache, dass die parallelen "Flächen" nach dem Abschneiden vom Prisma jetzt andere sind als vorher. Die Grundfläche \(ABC\) des Prismas ist nun zu gar nichts mehr parallel, da ihre korrespondiere Deckfläche abgeschnitten wurde. Es bleibt aber die Kante \(CF\), die parallel zur (neuen) Grundfläche \(ADEB\) liegt. Ein Bild sagt hier mehr als tausend Worte.
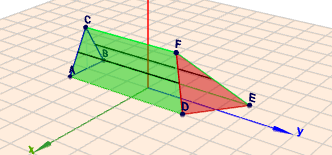
Klick auf das Bild und rotiere die Figur in Geoknecht3D mit der Maus. Dann erhältst Du einen guten räumlichen Eindruck. Mit der Parallelität von \(CF\) zu \(ADEB\) liegt wieder ein Prismatoid vor und es bleibt, die drei Flächen und die Höhe zu bestimmen. Die Höhe \(h\) ist die Höhe des Punktes \(C\) über der Grundfläche \(ADEB\) und ist damit identisch mit der Höhe im gleichseitigen Dreieck \(\triangle ABC\). Also ist
$$h = \frac12 \sqrt{3} \cdot |AB| = \frac12 \sqrt{3} \cdot 8 = 4\sqrt{3} \approx 6,928$$
Die Deckfläche \(A_D\) ist die Kante \(CF\) und damit ist \(A_D=0\). Für die verbleibenden zwei Flächen zunächst eine Skizze von oben
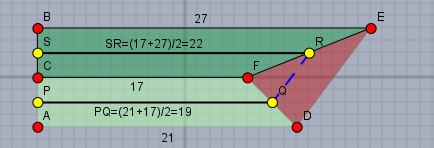
Die Grundfläche \(A_G\) ist das Trapez \(ADEB\), was mit der Flächenformel für Trapeze berechnet werden kann.
$$A_G = \frac{|AB|}{2}(|AD|+|EB|) = \frac{8}{2}(21 + 27) = 192$$
Die mittlere Fläche \(A_M\) ist ebenfalls ein Trapez. Ich habe das hier mit den gelben Punkten markiert: \(PQRS\). Jeder dieser Punkte liegt jeweils in der Mitte zweier Eckpunkte des Prismatoiden. So ist \(P\) die Mitte von \(AC\) und \(Q\) die Mitte von \(DF\). Das heißt auch, dass \(PQ\) die Mittelparallele des Trapez \(ADFC\) und \(SR\) die Mittelparallel von \(CFEB\) ist. Damit kann man nun \(A_M\) als Fläche des Trapez \(PQRS\) berechnen:
$$A_M = \frac{|PS|}{2}(|PQ|+|SR|) = \frac{4}{2}(19 + 22) =82$$
Jetzt nur noch in die Volumenformel einsetzen:
$$V = \frac{h}{6}(A_G + 4\cdot A_M + A_D) = \frac16 4\sqrt{3} (192 + 4\cdot 82 + 0) = \frac{1040}{3} \sqrt{3} \approx 600,4$$