Herleitung der Kreisgleichung über eine spezielle Determinante

Question

Hallo liebe Leute, mich beschäftigen immer noch Determinanten. Im Folgenden soll ich zeigen, dass man eine Kreisgleichung eindeutig darstellen kann, mittels:

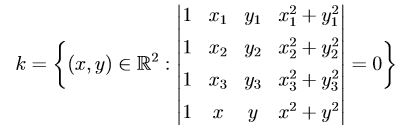
Wobei drei Punkte P(xi|yi) mit i aus {1,2,3} vorgegeben sind und nicht auf einer Geraden liegen. (Was passiert eigentlich wenn sie auf einer Geraden? Dann müsste doch die Unterdeterminante (3x3 links oben = 0 sein und wir hätten eine Gerade))

Jedenfalls hab ich mal losgerechnet und nach Laplace und Umformungen hab einen elends langen Ausdruck als Determinante bekommen (12 Summanden mit je 4 Faktoren). Ich weiß auch nicht, was das mit der Kreisgleichung zu tun haben sollte. Kann mir einer bitte helfen, wie man klug an diesen Beweis rangehen könnte?

LG Mathstiger

Answer 1

Eine Kreisgleichung in 2D hat die Form $$a(x^2+y^2)+bx+cy+d=0$$ mit \(a\ne0\). Entwickle die Determinante nach der letzten Zeile und zeige damit, dass die angegebene Gleichung diese Form hat und ausserdem von den drei vorgelegten Punkten erfuellt wird.