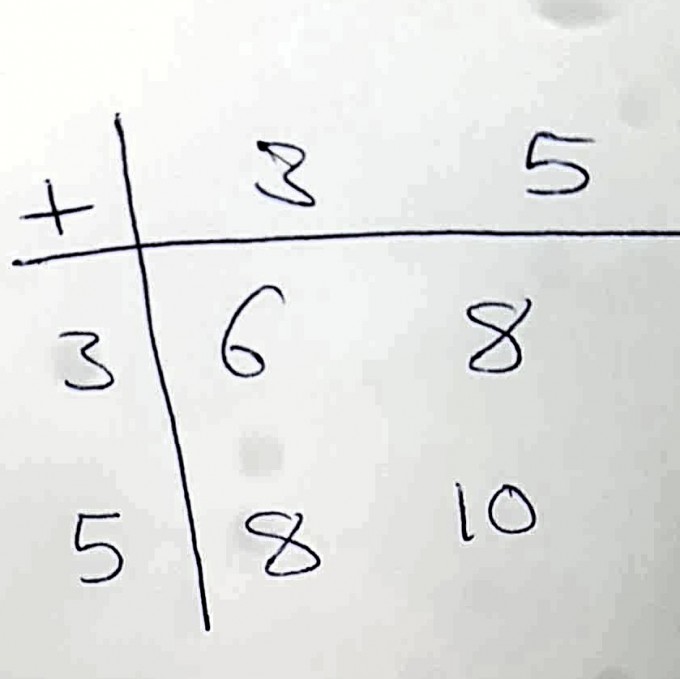Untermonoid bestimmen

Question

Ich muss das von {3, 5} erzeugte Untermonoid von N"natüliche Zahlen" bestimmen, d.h. die kleinste Menge
M ⊆ N, so dass {3, 5} ⊆ M und M bezüglich der Addition ein Monoid ist.

kann mir jemand sagen, was für Technik da gebraucht wird.

Ich hab das mit eine Tabelle gemacht, die in dem Foto steht, aber keine Ahnung ob ich das richtig gemacht oder falsch ?

für die Hinweise.

Comments

Ok, auf diese Weise hast du weitere drei Elemente gefunden...

...wie könnte es weitergehen?

---

keine Ahnung, aber vielleicht noch eine neue Tabelle mit die neue Elemente, meinst du ?

---

Na, das würde doch eine sehr große Tabelle werden, denn jeder neue Tabelleneintrag ist ja auch wieder Element des Untermonoids. Gesucht ist eine geschlossene Darstellung dieses unendlich großen Monoids. Beachte auch, dass die 0 auch enthalten ist.

Answer 1

Eine Woche ist rum, dann wollen wir mal auflösen:
M = {0, 3, 5, 3+3, 3+5, 5+3, 5+5, …, 3*a + 5*b}
Oder anders ausgedrückt: 
M = {3a+5b | a, b ∈ ℕ₀}