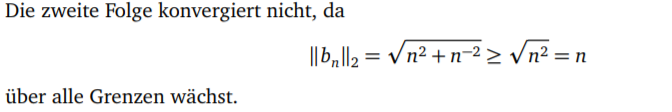Konvergiert folgende Folge?

Question

die Aufgabe lautet wie folgt:

x

die Aufgabe lautet wie folgt:
Ich habe versucht es wie folgt zu lösen, bei den ersten beiden Folgen hat das auch so geklappt aber bei der dritten scheint meine Lösung falsch zu sein, aber ich sehe den Fehler nicht :/

Answer 1

Teilaufgabe b)

a_n konvergiert gegen ( 0 ; 0 ).

bn konvergiert nicht ( 1. Komponente geht gegen unendlich )

cn pendelt immer zwischen (1;-1) und ( -1 ; 1 ) , konvergiert also auch nicht.

Comments

sry für die späte Rückfrage. Es reicht also bei Aufgaben wo ein Vektor aus Folgen gegeben ist, wenn nur eine 'Koordinate' divergiert damit die komplette Funktion divergiert. Andersherum müssen beide Koordinaten konvergieren damit die Funktion konvergiert. Habe ich das so richtig verstanden?

---

Es reicht also bei Aufgaben wo ein Vektor aus Folgen gegeben ist, wenn nur eine 'Koordinate' divergiert, damit die komplette Folge divergiert.

ja.

Andersherum müssen beide Koordinaten konvergieren, damit die Folge konvergiert. Habe ich das so richtig verstanden?

ja.

(zumindest, wenn die angegebene Metrik benutzt wird)

Answer 2

Deine Rechnung zu c_n

die euklidische Norm ist immer gleich. Aber die Vektoren ändern sich mit jedem Schritt. Schreibe mal ein paar Vektoren hin und beschreibe, was du siehst. 

Comments

also die Vektoren pendeln immer zwischen (-1 | 1)^t und (1 | -1)^t , das ist mir klar, aber ich dachte man müsste es so berechnen, dass man x und y in die euklidische Norm einsetzt und dann den Grenzwert berechnet, sonst wäre die euklidische Norm in der Aufgabe völlig überflüssig, da sie bei der c) sowieso nochmal definiert wird ...

So wie für die zweite Folge

---

Die euklidische Norm sollst du nur anwenden, um zu untersuchen, ob die beiden Werte gleich sind.

Berechne erst  die Differenz der Vektoren. Dann kannst du davon die Norm bilden. Diese sollte gegen 0 konvergieren (Das ist eine zwingende Voraussetzung für Konvergenz).

---

"Die euklidische Norm sollst du nur anwenden, um zu untersuchen, ob die beiden Werte gleich sind" Welche zwei Werte...? Sry ich schein echte Wissenslücken zu haben bezüglich der Norm...

---

Die euklische Norm berechnet doch in dem Fall den Abstand von a/b/cn zum Ursprung oder nicht?

---

https://de.wikipedia.org/wiki/Grenzwert_(Folge)#Erläuterung_und_Definition 

gilt für Konvergenz. Die Betragsstriche müssen gemäss der geltenden Norm interpretiert werden.