Funktionenschar, Parameter k Nullstellen

Question

Liebe Community,

ich habe folgendes Mathe-Problem:

Gegeben ist die Funktionsschar f(x)=2x⁴-12x²+k.

Nun sollen die Werte ermittelt werden, die der Parameter k annehmen muss, damit die Funktion keine bzw. zwei Nullstellen hat. Als Hinweis ist noch gegeben, dass die Funktion zwei Tiefpunkte, jeweils mit dem Funktionswert y=-2 hat.

Kann mir hier bitte jemand helfen oder einen Ansatz vermitteln? Ich weiß leider absolut nicht wie ich anfangen soll. Bin über jede Hilfe sehr dankbar.

Liebe Grüße

Jessy

Answer 1

f(x) = 2·x^4 - 12·x^2 + k

f'(x) = 0 --> x = √3

f(√3) = k - 18 > 0 --> k > 18

Für k > 18 gibt es also keine Nullstellen

Genau zwei Nullstellen damit genau für k = 18.

Welche Anzahl an Nullstellen gibt es noch und wie lauten die Bedingungen für k dafür?

Comments

Vielen Dank für die Hilfe. Konnte den Weg nachvollziehen und kam nun auf exakt zwei Nullstellen, wie finde ich nun aber heraus welchen Wert ich brauche, damit ich keine Nullstelle habe? Habe versucht, das Ganze analog anzuwenden, aber bekomme immer wieder Nullstellen heraus?!

---

Hab es doch selbst herausgefunden!

Answer 2

Gegeben ist die Funktionsschar f(x)=2x^4-12x^2+k.
Nun sollen die Werte ermittelt werden, die der
Parameter k annehmen muss, damit die Funktion
keine bzw. zwei Nullstellen hat.

Hier meine Berechnungen

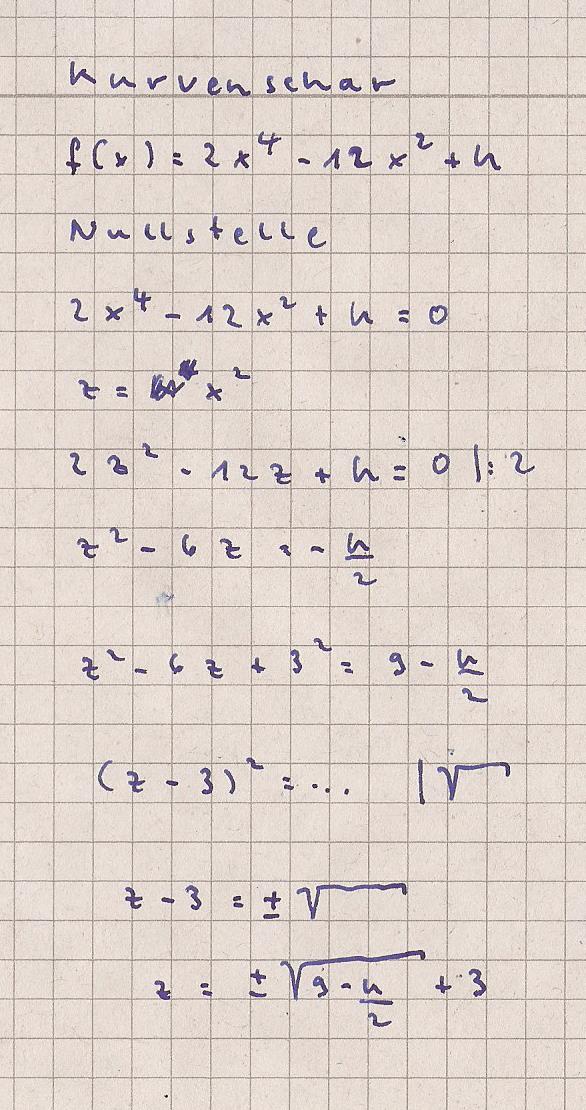
3 Fälle sind zu unterscheiden

1.)
9 - k/2 > 0 : Der Radikand ist positiv.
k < 18
Es gibt zwei Lösungen
z = ± √ ( 9 - k/2 ) + 3

2.)
9 - k/2 = 0 : Der Radikand ist null
k = 18
Es gibt 1 Lösung
z = 3

3.)
9 - k/2 < 0 : Der Radikand ist negativ
k > 18
Es gibt keine Lösung

Rückersetzen
x^2 = ± √ ( 9 - k/2 ) + 3

Muß noch weiter bearbeitet werden.

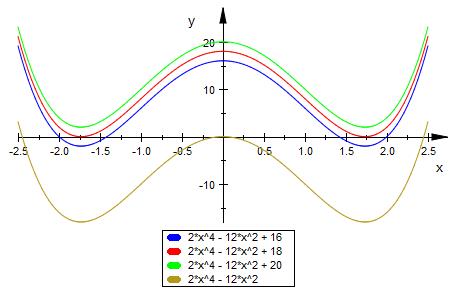
k > 18 : keine Nullstelle
k = 18 : 2 Nullstellen
0 < k < 18 : 4 Nullstellen
k = 0 : 3 Nullstellen
k < 0 : 2 Nullstellen

Jo mei.

Comments

Stell einmal ein Foto des Aufgabentextes ein.
Ich habe Zweifel an der Korrektheit deines
Aufgabentextes.