Wenn n ungerade ist und a ij = − a ji für alle i, j ∈{ 1 , ..., n } gilt, dann ist A nicht invertierbar?

Question

Ich habe keinen Ansatz, wie ich die Aufgabe lösen könnte. Wir hatten in der letzten Vorlesung Eigenwert, Eigenvektor, diagonalisierbarkeit. Aber ich weiß nicht wie diese Sachen mir bei der Lösung der Aufgaben behilflich sein kann.

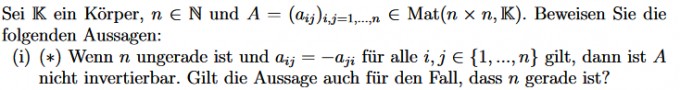
Vielen Dank im Voraus.

Comments

Tipp: det(A) = det(-A^T) = (-1)ⁿ·det(A^T) = (-1)ⁿ·det(A).

Answer 1

Hi, es gilt

$$    A^T = -A $$ und damit gilt $$ \det(A^T) = \det(A) = (-1)^n \det(A)   $$ also gilt $$   2 \cdot \det(A) = 0 $$ für ungerade n. Damit ist A nicht invertierbar. Für gerades n ist die Matrix 

$$ \begin{pmatrix} 0 & 1 \\ -1 & 0  \end{pmatrix} $$ ein Gegenbeispiel.

Comments

Wird nicht eine zusätzliche Voraussetzung an den Körper \(\mathbb K\) benötigt?

---

Ja klar, Charakteristik ungleich 2