Zunächst bin ich noch die Formel schuldig, mit der obige Wahrscheinlichkeiten berechnet wurden. Hier ist sie:
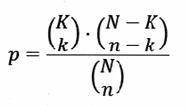
Dabei ist N = 52 (alle Karten), n = 4 (Anzahl der Asse),
K = 20 (Anzahl der verteilten Karten) und k = 2 (bzw. 3, bzw. 4 - Anzahl der verteilten Asse).
Den Binomialkoeffizient setze ich als bekannt voraus.
Jetzt kann man weiterrechnen indem man die so berechneten Wahrscheinlichkeiten mit der Wahrscheinlichkeit multipliziert, mit der ein Spieler ein zweites As bekommt. Also mit \( \frac{1}{19} \) , bzw \( \frac{2}{19} \) , bzw. \( \frac{3}{19} \) . Dann erhält man folgende Wahrscheinlichkeiten:
p(Fall 1) ≈ 0,018 p(Fall 2) ≈ 0,014 p(Fall 3) ≈ 0,003
Addiert man diese Werte, so erhält man die Lösung der Aufgabe:
p ≈ 0,035 ≡ 3,5%
100% sicher bin ich mir aber noch nicht. Auf jeden Fall gibt es noch eine weitere, kompliziertere Lösungsmöglichkeit.