Differentialgleichung: y´=xy+14y+3x+42, anhand Bedingung y(0)=25, ich soll das Anfangswertproblem y lösen

Question

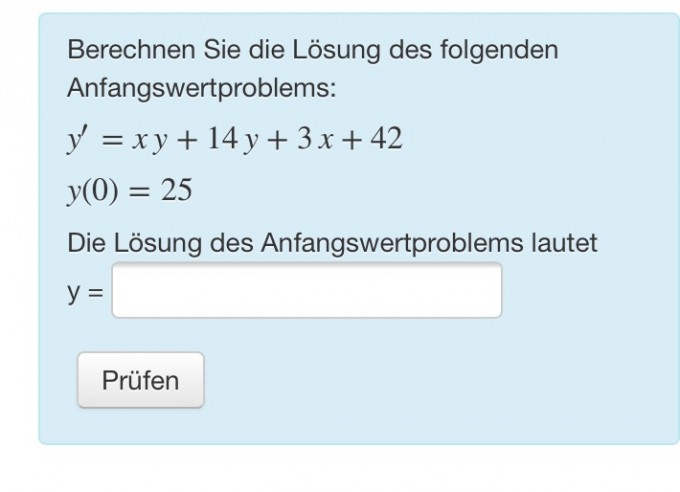
Anfangswertproblem wird oft auch spezielle Lösung genannt

Ich hab die Funktion integriert und erlange als allgemeine Lösung(falls korrekt):

y= e^{1/2x^3+14x}*e^C -2

Wie gehe ich nun danach vor bzw. stimmt meine allgemeine Lösung?

Danke euch und schönen Feiertag!

Answer 1

Ich bekomme   y ' = (y+3)*(x+14) und nach Integration

 y= e^{1/2x^2+14x}*e^C - 3

und dann

25 = e^C - 3

28 = e^c

c = ln(28) .

Also    y= 28*e^{1/2x^2+14}x - 3 

Answer 2

\( y=c_{1} \cdot e^{\frac{x^{2}}{2}+14 x}-3 \)

\( y(0)=25: \)
\( 25=c_{1} e^{0}-3 \)
\( c_{1}=28 \)
\( y=28 e^{\frac{x^{2}}{2}+14}-3 \)

Comments

Hallo, muss man wenn man hier den Betrag auf der linken Seite auflöst etwas beachten?