Lineare Optimierung - Firma erzeugt 2 Artikel an 3 Anlagen

Question

mir wurde folgende Aufgabe gestellt:

Firma erstellt P1 und P2.

P1 benötigt an Anlage 1 0.5h, an Anlage 2 2h, an Anlage 3 1.5h.

P2 benötigt an Anlage 1 2h, an Anlage 2 3h, an Anlage 3 0.5h.

Anlage 1 steht 12h zur Verfügung, Anlage 2 23h und Anlage 3 12h.

Gewinn pro P1 beträgt 2000€ und pro P2 4000€.

Wie viele Artikel von P1 und P2 müssen hergestellt werden, damit der Gewinn maximal wird?

Ich bin nun wie folgt vorgegangen:

	P1	P2	Gesamt
M1	0.5	2	12h
M2	2	3	23h
M3	1.5	0.5	12h

Folgende Restriktionen habe ich erstellt:

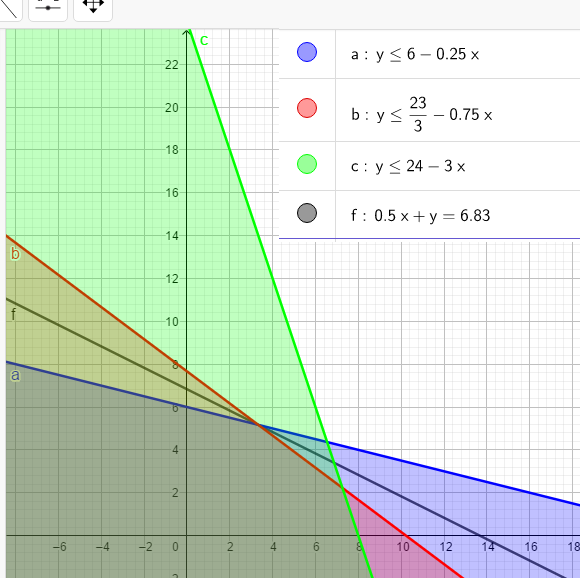
(1) 0.5x + 2y <= 12      |   y <= 6 - 0.25x

(2) 2x + 3y <= 23         |   y <= 23/3 - 0.75x

(3) 1.5x + 0.5y <= 12   |   y <= 24 - 3x

Zielfunktion lautet:

z = 2000x + 4000y     | y = (1/4000)z - 0.5x

Wenn ich nun alles graphisch einzeichne, stimmt die Zielfunktion absolut gar nicht. Irgendwas mache ich also total falsch, weiß jemand was? :-)

Answer 1

Deine Gleichung (2) ist falsch umgestellt. Musst Du für ggb auch nicht machen - die Darstellung kannst Du per rechtsklick ändern...

Hier https://www.geogebra.org/m/mddHVdbM und unter Wissensartikel findest Du eine Musteraufgabe.

oder per Simplex-Algorithmus

Comments

Vielen Dank für eure Antworten.

Dann war ich doch nicht so falsch wie ich dachte, bis auf die "Flüchtigkeitsfehler". :-)

---

Du bist auch dem richtigen Weg - wenn Du einen Fehler erkennst!

Ich lege die Zielfunktion immer auf einen Schieberegler (zmax), dann kann man die Zielfunktion schön ranschieben...

Viel Erfolg!

Answer 2

Ich löse indem ich die Schnitt- / Eckpunkte
der grauen Fläche in die Zielfunktion
einsetze
In etwa
( 0 | 6 ) 2000*0 + 4000*6 = 24000
( 3 | 5 ) 2000*3 + 4000* 5 = 26000
( 6 | 2.3 ) 2000*6 + 4000* 2.3 = 21200
( 8 | 0 ) 2000*8 + 4000*0 = 16000

Der Schnittpunkt von rot und blau
verspricht den meisten Gewinn.

Das hast du doch auch heraus.
Olivfarbene Zielfunktion.

Comments

Müsste aber normal nicht ein viel höherer Wert entstehen?

Wenn ich z.b P2 auf Anlage 3 , 12 Stunden produzieren lasse, hätte ich ja schon einen Ertrag von über 96000€. (12*0.5*4000€)

Falls jetzt alle 3 Anlagen produzieren, müsste ich doch eigentl. im 6-stelligen Betrag etwas rausbekommen.

Also in der Aufgabenstellung wurde nirgendwo erwähnt, das jedes Produkt alle Anlagen durchlaufen muss, gehe deshalb davon aus, dass alle Produkte paralell produziert werden können.

---

P1 benötigt an Anlage 1 0.5h, an Anlage 2 2h, an Anlage 3 1.5h.

P2 benötigt an Anlage 1 2h, an Anlage 2 3h, an Anlage 3 0.5h.

Dies isr sprachlich nicht eindeutig,
gemeint ist aber

P1 benötigt an Anlage 1 0.5h und an Anlage 2 2h und an Anlage 3 1.5h.
P2 benötigt an Anlage 1 2h und an Anlage 2 3h und an Anlage 3 0.5h.

Also wie in deiner und in meiner Lösung angenommen.
Bei den Lösungen ist darauf zu achten das nur
ganze Zahlen ( Stück ) in Frage kommen.

( 4 | 5 ) ergibt 28000 max Gewinn.

---

Ich danke dir vielmals für deine Hilfe!

Dann habe ich mir umsonst noch 2 Stunden den Kopf zerbrochen. :-)

---

Deine Lösung war ok.

Man muß auch beim Lösen von Matheaufgaben
nicht immer mit dem Kopf durch die Wand wollen.
Morgen ist meistens auch noch ein Tag.