Hallo Yamina,
Ich nehme an, dass der Draht in dieser Weise gebogen werden soll:
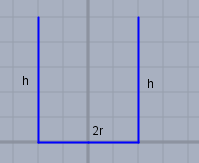
dann ist \(h + 2r + h = l = 110 \text{cm}\) bzw. \(h = l/2 - r\). Das Volumen soll maximal werden - es ist
$$V = h r^2\pi = (\frac{l}{2}-r) r^2 \pi = \frac{l}{2}r^2 \pi - r^3\pi$$ Ableiten nach \(r\) und Nullsetzen:
$$\frac{\text{d}V}{\text{d}r} = l r \pi - 3r^2\pi = 0 \quad \Rightarrow r = \frac{1}{3}l \approx 36,7 \text{cm}$$ und für die Höhe verbleiben dann \(h = l/2- l/3 = l/6 \approx 18,3 \text{cm}\)