Zunächst die Skizze ( symbolisch )
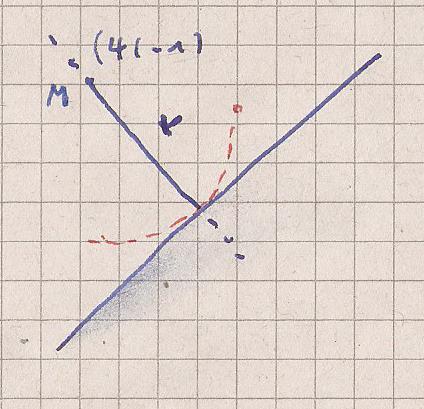
Der kürzeste Abstand ist der Radius r
Eine Tangente ist die Funktion
t ( x ) = -0.5 * x + 8
Eine Normale ist eine zur Tangente senkrecht
verlaufende Funktion.
Die Normale hat die Steigung
m2 = -1/m1 = - 1 / -0.5
m2 = 2
Die Normale geht durch den Mittelpunkt ( 4 | -1 )
-1 = 2 * 4 + b
b = -9
n ( x ) = 2 * x - 9
Schnittpunkt zwischen n und t
-0.5 * x + 8 = 2 * x - 9
2.5 x = 17
x = 6.8
y = 2 * 6.8 - 9
y = 4.6
( 6.8 | 4.6 )
r^2 = ( -1 - 4.6 ) ^2 + ( 4 - 6.8 )^2
r^2 = 39.2
r = 6.26