g ( x ) = - 2·x + 5 ;
p ( x ) = - x^2 + 3 ;
Die Diskussion hatten wir ja schon ein paar mal.
Ist der senkrechte Abstand oder der wirklich
kleinste Abstand. Falls ja wie soll die kleinste
Abstandsfunktion aufgestellt werden.
Ich bin für Version 2 aber über eine andere
Rechnung.
Verschiebe ich die Gerade parallel zur Parabel
hin wird sie den Punkt mit der Steigung -2 zuerst
berühren.
p ´( x ) = -2x
-2x = -2
x = 1
p ( 1 ) = - 1^2 + 3 = 2
( 1 | 2 )
Normale
m2 = -1 / m1 = -1 / -2 = 1/2
2 = 1/2 * 1 + b
b = 1.5
n ( x ) = 1/2 * x + 1.5
Muß ich gerade einmal zeichnen.
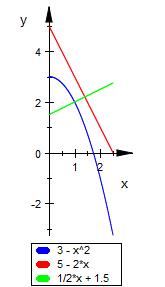
Schnittpunkt g = n
-2x + 5 = 1/2 * x + 1.5
-2.5x = -3.5
x = 1.4
p ( 1.4 ) = -2 * 1.4 + 5 = 2.2
( 1.4 | 2.2 )
Abstand zwischen
a^2 = ( 1.4 - 1 ) ^2 + ( 2.2 - 2 ) ^2
a = 0.447
Ich habe mir gerade die Frage nochmals
durchgelesen.
Meine Antwort geht glaube ich an der Frage
vorbei.
Gefragt ist irgendein beliebiger variabler Punkt
x auf p für den es die kleinste Abstandsfunktion
zu g zu ermitteln gilt.
Kann sein ich stelle später noch eine
Antwort ein.