Kern & Bild einer linearen Abbildung ( bestimmen

Question

Ich habe ein Problem bei folgender Aufgabe und hoffe, dass ihr mir dabei helfen könnt :)

Es geht um folgende Aufgabe:

EDIT: Vom Duplikat:
Titel: Abbildung von Polynome des Grades höchstens 3 nach R. Bild, Kern, Dim(bild), Dim(kern) bestimmen.
Stichworte: kern,abbildung,dimension
$$P_\mathbb R ^{(3)} -> \mathbb R,p-> \int_{-1}^1 \! p(x) \, \mathrm{d}x$$

Zu dieser Abbildung soll ich Bild, Kern und die Dimension der beiden bestimmen. Wie mache ich das? Ich bin mir selbst beim Bild unsicher wie ich das machen soll. Der einzige Ansatz den ich habe wäre über die Dimensionsformel zu gehen, aber bis ich dahin komme fehlen mir so oder so noch einige Schritte :/

Bezüglich dieser Aufgabe habe ich Fragen bei der a) und c). Diese stelle ich aber weiter unten.

Die b) habe ich versucht zu machen, aber ich bin mir nicht sicher, ob das, was ich da gerechnet habe, überhaupt Sinn ergibt. Hier ist mein Lösungsversuch für die b)

Gegeben: 

L_{2 :  $${ P }_{ R }^{ (3) }\longrightarrow R,\quad p\quad \mapsto \int _{ -1 }^{ 1 }{ p(x)dx } $$}

$$dim({ P }_{ R }^{ 3 })\quad =\quad n\quad +\quad 1\quad =\quad 3\quad +1\quad =\quad 4$$

$$p\quad \in { \quad P }_{ R }^{ (3) }\quad =\quad { a*x }^{ 3 }+{ b*x }^{ 2 }+{ c*x }^{ 1 }+d$$

Gesucht: 

Kern(L_j)

Bild(L_j)

dim(Kern(L_j))

dim(Bild(L_j))

Rechnung:

1. Schritt: Abbildungsvorschrift vereinfachen 

$$p\quad \mapsto \int _{ -1 }^{ 1 }{ p(x)dx } $$ = $$\quad { a*x }^{ 3 }+{ b*x }^{ 2 }+{ c*x }^{ 1 }+d\quad \mapsto \quad (\frac { a }{ 4 } { (1) }^{ 4 }\quad +\quad \frac { b }{ 3 } { (1) }^{ 3 }\quad +\quad \frac { c }{ 2 } { (1) }^{ 2 }\quad +\quad d*1)\quad -\quad \quad (\frac { a }{ 4 } { (-1) }^{ 4 }\quad +\quad \frac { b }{ 3 } { (-1) }^{ 3 }\quad +\quad \frac { c }{ 2 } { (-1) }^{ 2 }\quad +\quad d*(-1))$$

= $$\quad { a*x }^{ 3 }+{ b*x }^{ 2 }+{ c*x }^{ 1 }+d\quad \mapsto \quad \frac { 2*b }{ 3 } \quad +\quad 2*d$$

2. Schritt: Kern(Lj) berechnen 

Dafür müssen wir Koeffizienten finden so, dass $$\quad \frac { 2*b }{ 3 } \quad +\quad 2*d\quad =\quad 0$$

=> b = d = 0  und a und c kommen nicht vor.

Kern(L_{j) =}

 

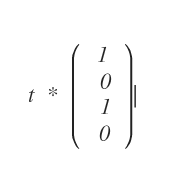
Ist das so richtig, oder bin ich komplett daneben ?

Für die a) und c) fällt mir kein Ansatz ein, weil die Notation mich die ganze verwirrt. Habt ihr da eine Idee?

Dome

Comments

Wieso folgerst Du aus \(\frac{2}{3}b+2d=0\), dass \(b=d=0\) sein muss? \(b=3\) und \(d=-1\) ist doch offensichtlich auch eine Lösung (unter vielen weiteren).

---

Stimmt, du hast recht. Wie kann man aber all diese Lösungen angeben ?

---

Mit linaren Gleichungssystemen sollte man sich an dieser Stelle schon auskennen. Du kannst eine Unbekannte als Parameter nehmen, sagen wir \(d\), und die andere in Abhaengigkeit davon ausdruecken, hier dann \(b=-3d\).

Ergebnis: Alle Polynome der Form \(ax^3-3dx^2+cx+d\) liegen im Kern von \(L_2\).

---

Achso! Okay, dann habe ich das verstanden. Mit Polynome tu ich mich da meistens schwer.

Noch eine Frage:

Der Grad des Polynoms des Kerns ist ja 3, somit ist die Dimension 4.

Nach der Dimensionsformel: dim V=dim ker(f)+dim im(f) ist ja die Dimension des Bildes

im(f) = dim V - dim ker(f) => im(f) = 4 - 4 = 0.   Ist die Dimension des Bildes also wirklich Null??

Denn wenn ich das Bild bestimmen muss, dann muss ich ja nur die Basis finden, die alle Polynome aus $$\int _{ -1 }^{ 1 }{ (a*{ x }^{ 3 }+\quad b*{ x }^{ 2 }\quad +\quad c*{ x\quad +\quad d })dx } $$

erzeugen können.

Und $$\int _{ -1 }^{ 1 }{ (a*{ x }^{ 3 }+\quad b*{ x }^{ 2 }\quad +\quad c*{ x\quad +\quad d })dx } $$

ist ja (wie oben brechnet) $$\frac { 2*b }{ 3 } \quad +\quad 2*d$$.

Diesen Term kann man trennen und man erhält

$$b*\frac { 2 }{ 3 } \quad +\quad 2*d$$. Und das wäre die "Basis" aller Flächen der Polynome 3. Grades, die durch das gegebene Integral berechnet werden. 

Ist das so richtig ? Wenn ja, dann welche Dimension hat das Bild dann? Ich habe nämlich kein x :/

---

Der Grad des Polynoms des Kerns ist ja 3, somit ist die Dimension 4.

Falsch geraten. Zwar sind die Polynome im Kern vom Grad ≤ 3, aber nicht alle Polynome vom Grad ≤ 3 liegen im Kern. Gib eine Basis des Kerns an und zaehle, wie viele Elemente die hat. Das bestimmt die Dimension, nicht der Polynomgrad.

---

Vom Duplikat:

Titel: Abbildung von Polynome des Grades höchstens 3 nach R. Bild, Kern, Dim(bild), Dim(kern) bestimmen.

Stichworte: kern,abbildung,dimension

$$P_\mathbb R ^{(3)} -> \mathbb R,p-> \int_{-1}^1 \! p(x) \, \mathrm{d}x$$

Zu dieser Abbildung soll ich Bild, Kern und die Dimension der beiden bestimmen. Wie mache ich das? Ich bin mir selbst beim Bild unsicher wie ich das machen soll. Der einzige Ansatz den ich habe wäre über die Dimensionsformel zu gehen, aber bis ich dahin komme fehlen mir so oder so noch einige Schritte :/

Answer 1

Hallo

 zu 2) da das Integral von -1 bis +1 geht ist direkt klar, dass es NUR 0 ergibt, wenn die fkt punktsymmetrisch zu 0 ist also für p)ax^3 +bx, damit ist deine Rechnung zwar überflüssig aber richtig.

zu 1 das Kreuzprodukt ist 0 wenn die 2 Vektoren parallel sind (kolinear) also a x r*a=0 damit hast du den kern und der ganze rest ist das Bild.

zu 3 v-w=0 wenn w=v ist.

du kannst ja eine Basis von V wählen,  dann werden alle gleichen Basisvektoren  auf 0 abgebildet .

 zur Vorstellung nimm V=R^2 du hast die Basis (1,0), (0,1) in V xV liegen dann alle Paare  (r*(1,0)+s*(0,1), q*(1,0)+v*(0,1)) r,s,q,v in R

sie werden auf 0 abgebildet wenn r=q,s=v ist.

wenn man nicht weiter kommt, ist es immer mal gut, ein einfaches Beispiel zu nehmen.

Gruß lul

Comments

da das Integral von -1 bis +1 geht ist direkt klar, dass es NUR 0 ergibt, wenn die fkt punktsymmetrisch zu 0 ist also für p)ax³ +bx

wenn man nicht weiter kommt, ist es immer mal gut, ein einfaches Beispiel zu nehmen.

Solltest du vielleicht auch selbst beherzigen.
\(\displaystyle\int_{-1}^1(3x^2-1)\,\mathrm dx=0\).

---

Hallo

Danke nn!  Du hast besser überlegt! (deshalb wohl die Fallunterscheidung?)

---

Danke für deine schnelle Antwort! Ich setze deine Tipps um und frage nach Bedarf nochmal nach!

lg

Dome