Definitionsbereich bestimmen

Question

ich habe eine Frage bezüglich der Funktion f(x). Wie ist der Definitionsbereich dieser Funktion?

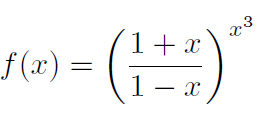
Habe den Nenner gleich Null gesetzt, also: 1 -x = 0. Ich stelle die Formel um und erhalte x = 1.

Also darf ich keine 1 einsetzen.

Dann wäre der Definitionsbereich alle Reellen Zahlen ohne die 1.

Schaue ich in die Lösung steht leider auch noch die -1. Kann mir jemand erklären wie ich dadrauf komme?

Answer 1

Für x = -1 ist der Exponent x³ = (-1)³ = -1 negativ.

Potenzen mit negativem Exponenten sind mittels Division definiert (a^-n := 1/aⁿ).

Also muss (x+1)/(x-1) ≠ 0 sein. Insbesondere muss x + 1 ≠ 0 sein.

Answer 2

x = -1
x ^3 = ( -1 ) ^3 = -1

( 1 + x ) / ( 1 - x ) = ( 1 + (-1) ) / ( 1 - (-1) ) = 0 / 2

( 0 / 2 ) ^{-1} = 2 / 0 | Division durch 0

D = R \ { x ± 1 }

Comments

Quatsch! Siehe:

https://www.wolframalpha.com/input/?i=((1%2Bx)%2F(1-x))%5Ex%5E3+domain

---

Quatsch! Siehe:

https://www.wolframalpha.com/input/?i=((1%2Bx)%2F(1-x))%5Ex%5E3,+x%3D-2