So ein Integral lässt sich nicht analytisch lösen, sondern nur numerisch.
Du könntest zum Beispiel eine Taylorapproximation durchführen. Oder du wendest eine der bekannten numerischen Integrationsmethoden an, zum Beispiel Trapez.
Oder man berechnet es mit einem Computer direkt, auch nur numerisch, nach dieser Abbildung:
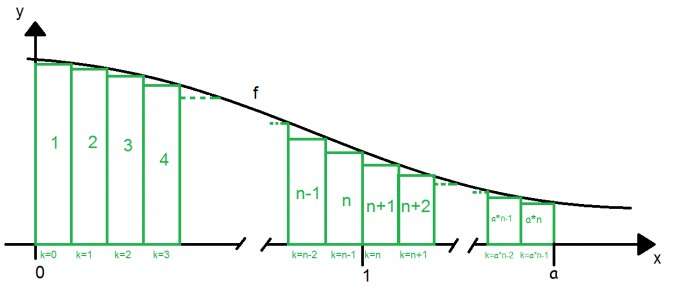
$$ A_k=\frac{1}{n}\cdot f(x),\text{ mit } x:=\frac{k}{n} $$
Dann hat man:
$$ \sum_{k=0}^{a\cdot n-1}{A_k}=\sum_{k=0}^{a\cdot n-1}{\frac{1}{n}\cdot f\Bigg(\frac{k}{n}\Bigg)}=\frac{1}{n}\cdot\sum_{k=0}^{a\cdot n-1}{ f\Bigg(\frac{k}{n}\Bigg)} $$
$$ f(x)=sin(x) \quad :\int_{0}^{\pi}{\sqrt{1+cos^2(x)}dx}\\\stackrel{n=10000}{\approx}\frac{1}{10000}\cdot\sum_{k=0}^{3,141\cdot10000-1}{\sqrt{1+cos^2\Big(\frac{k}{10000}\Big)}}\approx 3,819 $$
Bei pi muss man hier allerdings ,,schummeln'', was aber für große n widerum keine bedeutende Rolle mehr spielen würde.
Python-Code:
from math import*
n = int(input(' n = ')) #Einteilungsschritte
a = float(input(' a = ')) #Obergrenze
summe = 0
k=0 #Laufvariable k
while k<=a*n-1: #Es wird solange aufaddiert, bis diese Bedingung nicht mehr gilt
summe = summe+sqrt(1+cos(k/n)**2)
k = k+1
print(summe/n)
Alternativ kann man sich auch eine ganzrationale Funktion 4. Grades zusammenbasteln, die f annähern soll:
$$ p(x)=ax^4+bx^3+cx^2+dx+e\\ p'(x)=4ax^3+3bx^2+2cx+d $$
Diese soll folgende Eigenschaften mitbringen:
$$ 1.) p(0)=\sqrt(2)=f(0) \Rightarrow e=\sqrt{2} \\ 2.) p(\pi/2)=1=f(\pi/2) \\ 3.) p(\pi)=\sqrt{2}=f(\pi) \\ 4.) p'(0)=0=f'(0) \Rightarrow d=0 \\ 5.) p'(\pi)=0=f'(0)$$
Somit muss man nur noch folgendes Gleichungssystem lösen:
$$ 2.) \Big(\frac{\pi}{2}\Big)^4\cdot a+\Big(\frac{\pi}{2}\Big)^3\cdot b+\Big(\frac{\pi}{2}\Big)^2\cdot c=1-\sqrt{2}\\ 3.) \ \ \pi^4\cdot a+\pi^3 \cdot b+\pi^2 \cdot c=0 \\ 5.) \ \ 4\pi^3\cdot a+3\pi^2\cdot b+2\pi\cdot c=0 $$
Gelöst ergibt das :
$$ a=-\frac{16(\sqrt{2}-1)}{\pi^4} \\ b=\frac{32(\sqrt{2}-1)}{\pi^3} \\ c=-\frac{16(\sqrt{2}-1)}{\pi^2} \\ d=0 \\ e=\sqrt{2} $$
Also folgendes Näherungspolynom:
$$ p(x)=-\frac{16(\sqrt{2}-1)}{\pi^4}x^4+\frac{32(\sqrt{2}-1)}{\pi^3} x^3-\frac{16(\sqrt{2}-1)}{\pi^2}x^2 +\sqrt{2}. $$
Längenberechnung:
$$ \int_{0}^{\pi}{\sqrt{1+cos^2(x)}dx}\\ \approx \int_{0}^{\pi}{\Bigg(-\frac{16(\sqrt{2}-1)}{\pi^4}x^4+\frac{32(\sqrt{2}-1)}{\pi^3} x^3-\frac{16(\sqrt{2}-1)}{\pi^2}x^2 +\sqrt{2}\Bigg)dx}\\=\Bigg[-\frac{16(\sqrt{2}-1)}{5\pi^4}x^5+\frac{32(\sqrt{2}-1)}{4\pi^3} x^4-\frac{16(\sqrt{2}-1)}{3\pi^2}x^3 +\sqrt{2}x \Bigg]_{0}^{\pi}\approx 3.75 $$