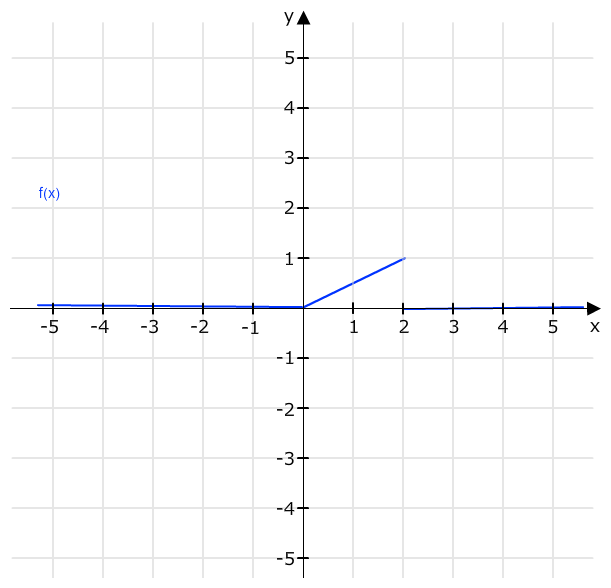
f(x)= 0 : x<0
kx : 0≤ x ≤ 2
0 : x≥ 2
zu einer Dichtefunktion einer stetigen Zufallsgröße wird?
Skizze:
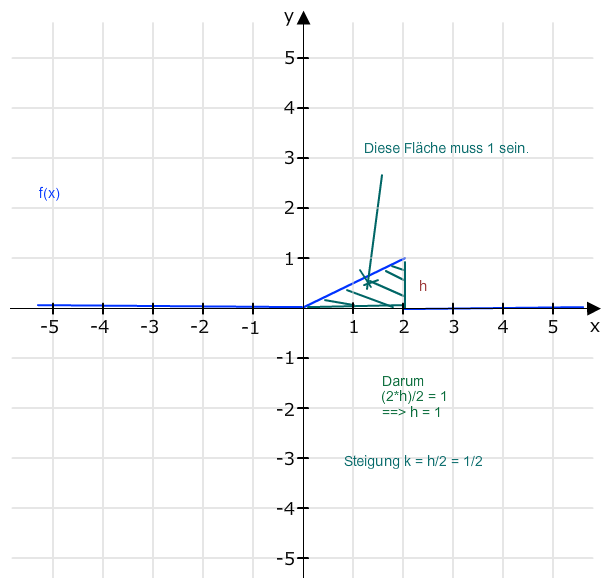
f(x)= 0 : x<0
1/2 x : 0≤ x ≤ 2
0 : x≥ 2
F(x) = 0 für x< 0
= 1/4 x^2 für 0 ≤ x≤ 2
= 1 für x≥ 2
E(x) = ∫_(-∞)^{∞} x·f(x) dx
= ∫_(0)^{2} x·1/2 x dx
= 1/2 ∫_(0)^{2} x^2 dx
= 1/2 [ 1/3 x^3 ]_(0)^{2}
= 1/2 ( 8/3 - 0)
= 4/3
(ohne Gewähr!)