momentane Änderungsrate des zweiten Arguments bei Erhöhung des ersten Arguments kontrolle

Question

Gegeben sei die Funktion

f(x,y) e^{-0,25x+0,2y+0,05yx}

Bestimmen Sie die momentane Änderungsrate des zweiten Arguments bei Erhöhung des ersten Arguments um eine marginale Einheit an der Stelle a=(1.2,2.9)
und unter Beibehaltung des Niveaus der Funktion F.

Bin mir nich sicher ob mein Rechenweg so stimmt, oder ob die Lösung so richtig ist,  kann mir jemand weiterhelfen?

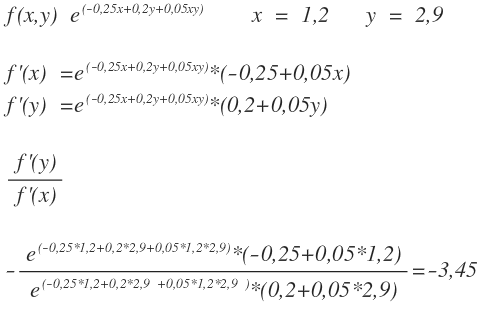
Lg

Answer 1

Schau mal, wie viele Fragen in den letzten 2 Tagen noch offen sind. https://www.mathelounge.de/unanswered

Das dauert halt eine Weile und die vielen "ähnlichen Aufgaben" deuten halt an, dass du dort selbst zu einer Antwort kommst.

Man sieht leider in der verlinkten Liste nicht, dass du tatsächlich schon ernsthaft etwas versucht hast. Ich habe dir dafür mal einen Daumen hoch gegeben.

Comments

werd es noch mal versuchen und die ähnlichen Fragen genauer anschauen, danke für den Daumen nach oben.

---

Scheint so als wäre mir ein Fehler unterlaufen als ich es ausgerechnet habe, also sollte 0,40 die richtige Lösung sein, bin aber nicht zu 100% sicher

-e^{-0.25*1.2+0.2*2.9+0.05*1.2*2.9}*(-0.25+0.05*2.9)/(e^{-0.25*1.2+0.2*2.9+0.05*1.2*2.9}*(0.2+0.05*1.2)

---

Außerdem: die richtige Antwort zu der Frage ist 0,4

Sehr gut, dann hat das wenigstens geklappt.