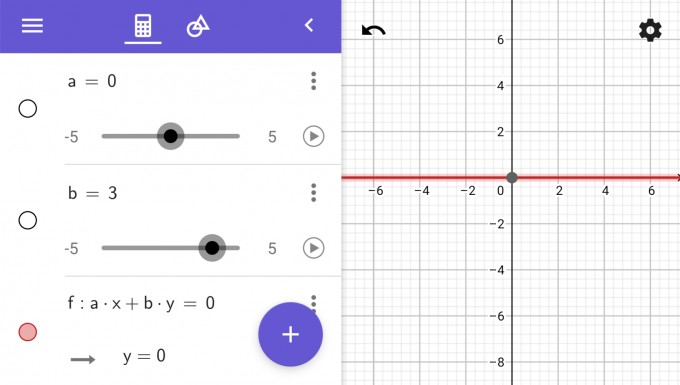
Falls a=0 und b≠0.
Dann sieht die Gleichung so aus: 0*x+b*y=0 ⇔ b*y=0 ⇔ y=0
Es ist also eine konstante Gerade, welche immer den Wert Null hat, sie liegt also in der x- Achse
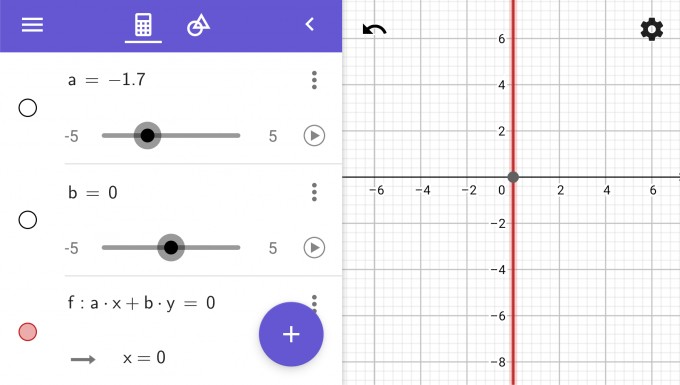
Falls a≠0 und b=0
Dann sieht die Gleichung so aus: a*x+0*y=0 ⇔ a*x=0 ⇔ x=0
Das ist nun eine um 90° gedrehte Gerade, die die Nullstelle 0 hat und in der y-Achse liegt.