Die Lösung einer quadratischen gleichung

Question

Hallo kann mir einer vielleicht in paar Sätzen erklären warum es bei q.gleichungen 2 ergebnisse gibt? Zb x²=121 = x1 ist 11 und x2  ist - 11.?

Und bestenfalls auch wann es nur eine Lösung gibt. Vielen dank !

Answer 1

Das liegt daran dass es jeden funktionswert 2mal gibt. Durch das quadrieren bekommt man aus x=3 und aus x=-3 den gleichen funktionswert nämlich y=9.

Answer 2

mach es doch mal umgekehrt:

11 *11= 121   oder 11² =121

(-11)*(-11) =121   oder (-11)² =121

wie du siehst kann man ein gleiches Ergebnis erzielen beim Quadrieren mit dem Vorzeichen  + und mir dem Vorzeichen -,

folglich muss man auch auf zwei Lösungen kommen wenn √ 121 berechnet nämlich ±11.

(Potenzrechengesetze

Answer 3

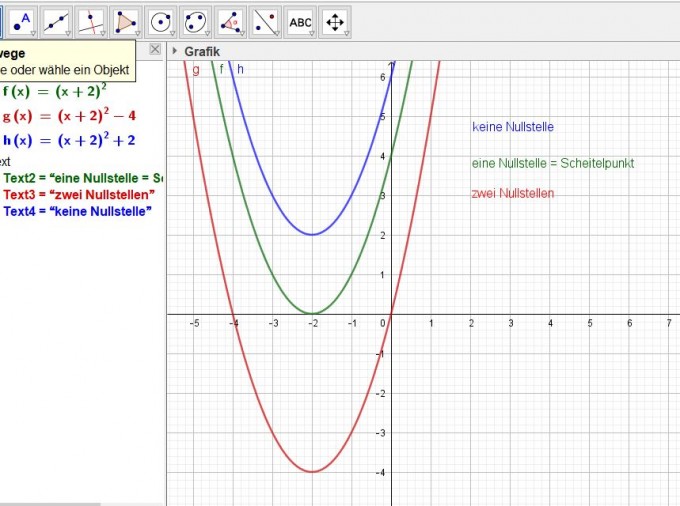
bei quadratischen Gleichungen werden oft die Nullstellen, also die Schnittpunkte mit der x-Achse gesucht. Wenn du die pq-Formel zur Lösung verwendest, ergeben sich

zwei Lösungen, wie Koffi es schon erklärt hat, wenn unter der Wurzel eine positive Zahl steht

eine Lösung, wenn die Wurzel null ergibt

keine Lösung, wenn unter der Wurzel eine nagative Zahl steht.