Mit der Hessenormalenform kann man einfacher den Abstand eines Punktes und einer Ebene berechnen, anstelle jedesmal eine Gerdengleichung aufstellen zu müssen, die senkrecht zur Ebene verläuft und durch den zu betrachtenen Punkt geht. Das kann ellegant umgangen werden, nämlich mit der Hessenormalenform
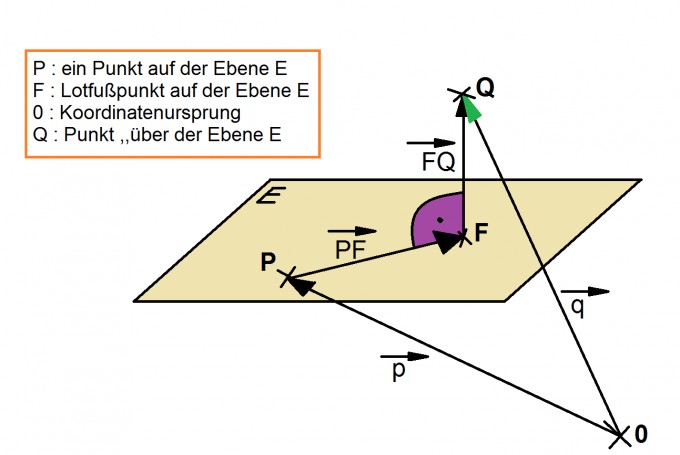
Das Ziel ist die Berechnung des Abstandes vom Punkt F und Q.
Ok. Du hast schonmal hier in der Skizze ein Problem, denn du kennst den Punkt F nicht, sondern nur P (Stützvektor der Ebene E) und dein Punkt Q über der Ebene. Das bedeutet, du muss einen ,,Umweg'' nehmen, um $$ |\vec{FQ}| $$ zu erhalten. Der Weg wäre folgendermaßen:
$$ \vec{FQ}=-\vec{PF}-\vec{p}+\vec{q}\qquad (*) $$
Ok ist immernoch blöd, da diese Gleichung immernoch von diesem nervigen Lotfußpunkt F abhängt...
Aber jetzt kommts! Die beiden Vektoren $$ \vec{PF} \text{ und } \vec{FQ} $$ stehen senkrecht zueinander, d.h ihr Skalarprodukt von ihnen ist Null. Man kann also nun den Vektor $$ \vec{PF} $$eliminieren, indem (*) mit $$\vec{FQ} $$multipliziert wird. Dann hat man also:
$$ \begin{aligned} \vec{FQ}&=-\vec{PF}-\vec{p}+\vec{q} &|\cdot \vec{FQ}\\ \vec{FQ}\cdot \vec{FQ}&=\vec{FQ}\cdot(-\vec{PF}-\vec{p}+\vec{q})\\ \vec{FQ}\cdot \vec{FQ}&=\vec{FQ}\cdot(\vec{q}-\vec{p})-\vec{FQ}\cdot \vec{PF}\\\vec{FQ}\cdot \vec{FQ}&=\vec{FQ}\cdot(\vec{q}-\vec{p})-0\\\vec{FQ}\cdot \vec{FQ}&=\vec{FQ}\cdot(\vec{q}-\vec{p})\end{aligned} $$Das Skalarproduktes eines Vektors mit sich selbst multipliziert ist das Quadrat des Betrages vom Vektor. Also darf man schreiben: $$ |\vec{FQ}|^2=\vec{FQ}\cdot(\vec{q}-\vec{p}) $$Und damit gilt auch:
$$ |\vec{FQ}|\cdot |\vec{FQ}|=\vec{FQ}\cdot(\vec{q}-\vec{p}) \quad |:|\vec{FQ}|\\\underline{\underline{|\vec{FQ}|=\frac{\vec{FQ}}{|\vec{FQ}|}\cdot(\vec{q}-\vec{p})}} $$
Der entstandene Quotient $$ \frac{\vec{FQ}}{|\vec{FQ}|} $$ ist der Normalenvektor zur Ebene E in normierter Form. Damit ist denke ich wohl deine Frage zu Genüge beantwortet worden.
Ach noch etwas. Die rechte Seite der entstandenen Abstandsformel kann negativ werden. Das ist aber für Abstände Blödsinn, weshalb man den Betrag nimmt. Dann sieht die fertige Hesse'sche Normalenform (kurz HNF) so aus:
$$ d(F;Q)=\Bigg |\vec{n}\cdot(\vec{q}-\vec{p}) \Bigg|, \text{ mit } \vec{n}=\frac{\vec{FQ}}{|\vec{FQ}|} $$
Das heißt den Normalenvektor auf 1 normieren zu müssen ist einfach eine Folge von der Herleitung dieser Abstandsformel.