Gegeben f(x)=-1/2x² +2x+2 und Geraden durch P(-1|0). Schnittwinkel und Tangenten gesucht.

Question

Gegeben ist die Funktion f(x)=-1/2x²+2x+2.

a) Eine Gerade durch den Punkt P(-1|0) schneidet den Graphen von f an der Stelle x=3. Geben Sie die Geradengleichung und die Größe des Schnittwinkels an.

b) Welche Gerade durch den Punkt P(-1|0) ist Tangente an den Graphen von f. Zeichnen Sie den Graphen und die Tangente.

Answer 1

f(x) = -1/2·x^2 + 2·x + 2

a) Eine Gerade durch den Punkt P(-1|0) schneidet den Graphen von f an der Stelle x=3. Geben Sie die Geradengleichung und die Größe des Schnittwinkels an.

f(3) = 3.5 --> Q(3 | 3.5)

Gerade durch P und Q

m = (Qy - Py) / (Qx - Px) = (3.5 - 0) / (3 - (-1)) = 3.5 / 4 = 0.875

g(x) = m·(x - Px) + Py = 0.875·(x - (-1)) + 0 = 0.875·(x + 1) = 0.875·x + 0.875

f'(x) = 2 - x

g'(x) = 0.875

α = arctan(f'(3)) - arctan(g'(3)) = arctan(-1) - arctan(0.875) = -45 - 41.18592516 = -86.18592516

Der Schnittwinkel beträgt etwa 86.19°

b) Welche Gerade durch den Punkt P(-1|0) ist Tangente an den Graphen von f. Zeichnen Sie den Graphen und die Tangente.

(f(x) - 0) / (x - (-1)) = f'(x)
(- 0.5·x^2 + 2·x + 2) / (x + 1) = 2 - x
- 0.5·x^2 + 2·x + 2 = (2 - x)·(x + 1)
- 0.5·x^2 + 2·x + 2 = - x^2 + x + 2
0.5·x^2 + x = 0
x = -2 ∨ x = 0

t1(x) = f'(-2) * (x + 2) + f(-2) = 4·x + 4
t2(x) = f'(0) * (x + 0) + f(0) = 2·x + 2

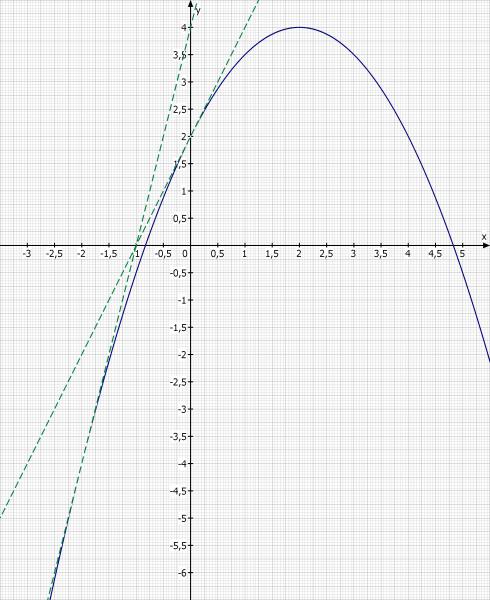
Skizze

Answer 2

Gegeben ist die Funktion f(x)=-1/2x²+2x+2.

a) Eine Gerade durch den Punkt P(-1|0) schneidet den Graphen von f an der Stelle x=3. Geben Sie die Geradengleichung und die Größe des Schnittwinkels an.

f(3) = -1/2*9 + 6 + 2 = 8 -4.5 = 3.5

g: y = mx + q

0 = -m + q ---> m=q

g: y = mx + m

3.5 = 3m + m = 4m

3.5/4 = m

7/8 = m

g: y = 7/8 x + 7/8

Noch nochrechnen!

b) Welche Gerade durch den Punkt P(-1|0) ist Tangente an den Graphen von f. Zeichnen Sie den Graphen und die Tangente.

Wieder gilt wegen P

y = mx + m

-1/2x²+2x+2 = mx + m             hat genau eine Lösung

0= 0.5 x^2 + (m-2)x + (m-2)

Diskriminante d = b^2 - 4ac Null setzen

d= (m-2)^2 - 2(m-2) = m^2 - 4m + 4 - 2m + 4 = m^2 - 6m + 8 =0 .

m1,2 = 1/2 ( 6 ± √(36 - 32)) = 1/2( 6±2)

m1 = 4

m2 = 2

t1: y = 4x + 4

t2: y = 2x +2

Hier ebenfalls sorgfältig nachrechnen und Rechenfehler bitte melden.