Graphen verschieben, sodass sie die Tangente in zwei Punkten berührt

Question

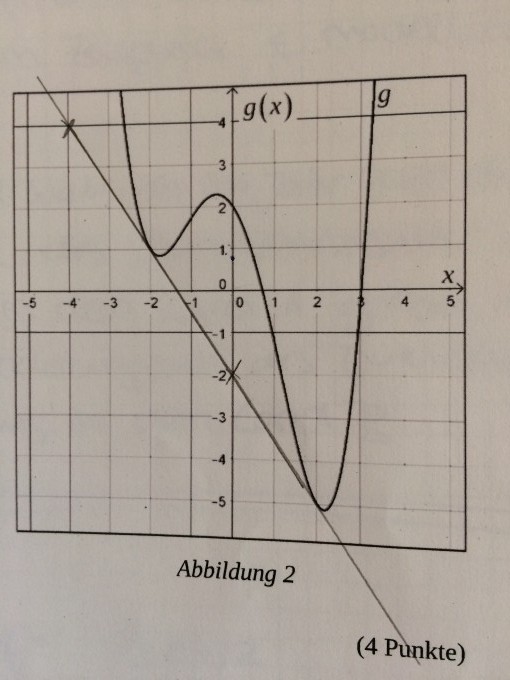
Der Graph von g mit g(x)= 1/4x^4 - 2x^2 - 3/2x +2 wird um 2 Einheiten nach rechts verschoben.

Der verschobene Graph wird anschließend do weit nach unten verschoben, bis die Gerade t mit y= - 3/2x - 2 in zwei Punkten Tangenten an den neuen Graphen ist.

Geben Sie an, um wieviele Einheiten der nach rechts verschobene Graph dazu nach unten verschoben werden muss, und begründen Sie Ihre Angabe.

PS: Als Anlage liegt hierbei noch eine Abbildung fest Graphen mit der Tangente bei

Natürlich kann man auf der Abbildung sehen dass der Graph um 3 Einheiten nach unten verschoben werden müsste aber gibt es auch einen Rechenweg wie man dies ohne die Abbildung herausfinden könnte?

Answer 1

x-2 für x einsetzen. Ableiten. Wo ist diese Ableitung gleich-3/2? Diese Stellen in die um b nach oben verschobene Tangentengleichung und die Polynomgleichung einsetzen. Wie groß muss b sein?

Comments

Kannst du deine Antwort noch in einen Kommentar umwandeln?

Hier mal die um 2 Einheiten nach rechts verschobene Kurve:

~plot~ g(x)= 1/4 x^{4} - 2 x^{2} - 3/2 x +2; 1/4 (x-2)^{4} - 2 (x-2)^{2} - 3/2 (x-2) +2 ~plot~