das ist eine von den Aufgaben, die im Grunde leicht zu lösen sind, wenn man nur die Aufgabenstellung genau versteht. Gesucht ist eine Matrix - ich nenne sie mal \(A^*\) - die die gleiche Abbildung darstellen soll wie \(A\); nur auf ein anderes Koordinatensystem bezogen.
Das andere System - ich nenne es mal \(1\) - ist durch seine Einheitsvektoren gegeben. Diese sind im Standardsystem - ich nenne das mal \(0\) - definiert. Es ist
$$^0T_1 = \frac{1}{\sqrt{10}}\begin{pmatrix} 1 & -3 \\ 3 & 1\end{pmatrix}$$
das bedeutet, dass eine Position \(^1p\) mit Hilfe dieser Transformationsmatrix nach \(^0p\) transformiert werden kann. Achtung! die Position selbst ist die gleiche, nur ihr Bezugssystem ändert sich. Ein Bild soll das veranschaulichen.
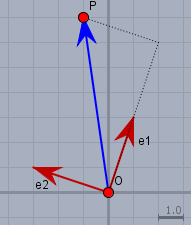
Der Einfachheit halber habe ich eine Transformationsmatrix
$$^0U_1 = \begin{pmatrix} 1 & -3 \\ 3 & 1\end{pmatrix}$$
also ohne den Faktor \(1/\sqrt{10}\), gewählt. Du siehst dort den Punkt \(P\) der im 0-System die Koordinaten
$$^0p=\begin{pmatrix} -1 \\ 7 \end{pmatrix}$$ hat. Im 1-System erreicht man den Punkt, indem man ausgehend vom Ursprung 2mal in Richtung \(e_1\) marschiert und anschließend 1mal in Richtung \(e_2\) - also sind die Koordinaten von \(P\) im 1-System
$$^1p=\begin{pmatrix} 2 \\ 1 \end{pmatrix}$$ und man rechnet dies, indem man die Transformationsmatrix mit dem Vekor multipliziert
$$^0p = {^0U_1} \cdot {^1p} = \begin{pmatrix} 1 & -3 \\ 3 & 1\end{pmatrix} \cdot \begin{pmatrix} 2 \\ 1 \end{pmatrix} = \begin{pmatrix} -1 \\ 7 \end{pmatrix} $$ oder auch
$$^1p= {^1U_0} \cdot {^0p}$$ wobei
$$^1U_0 = \left( {^0U_1}\right)^{-1}$$ ist. So das war nur das Vorgeplänkel; kommen wir zur eigentlichen Aufgabe.
Gesucht ist eine Matrix \(A^*\), die die gleichen Abbildung erzeugt wie \(A\), nur dass die Positionen im 1- statt im 0-System gegeben sind. Es soll also sein
$$^1p' = A^* \cdot {^1p}$$
jetzt transformiere ich in das 0-System (s.o.)
$$ ^1T_0 \cdot {^0p'} = A^* \cdot {^1T_0} \cdot {^0p}$$ und multipliziere links \(^0T_1\)
$$ {^0p'} = {^0T_1} \cdot A^* \cdot {^1T_0} \cdot {^0p}$$ das \({^0p'}\) ist aber lt. Aufgabenstellung
$${^0p'} = A \cdot {^0p}$$
und das muss für jeden beliebigen Punkt \({^0p}\) passen, folglich muss sein:
$$A = {^0T_1} \cdot A^* \cdot {^1T_0}$$
bzw.:
$$\begin{aligned} A^* &= {^1T_0} \cdot A \cdot {^0T_1} \\ &= \frac{1}{\sqrt{10}}\begin{pmatrix} 1 & 3 \\ -3 & 1\end{pmatrix} \cdot \begin{pmatrix} 1 & -5 \\ 3 & 9\end{pmatrix} \cdot \frac{1}{\sqrt{10}}\begin{pmatrix} 1 & -3 \\ 3 & 1\end{pmatrix} \\ &= \begin{pmatrix} 7,6 & -0,8 \\ 7.2 & 2,4\end{pmatrix} \end{aligned}$$
falls noch Fragen offen sind, so melde Dich bitte.
Gruß Werner