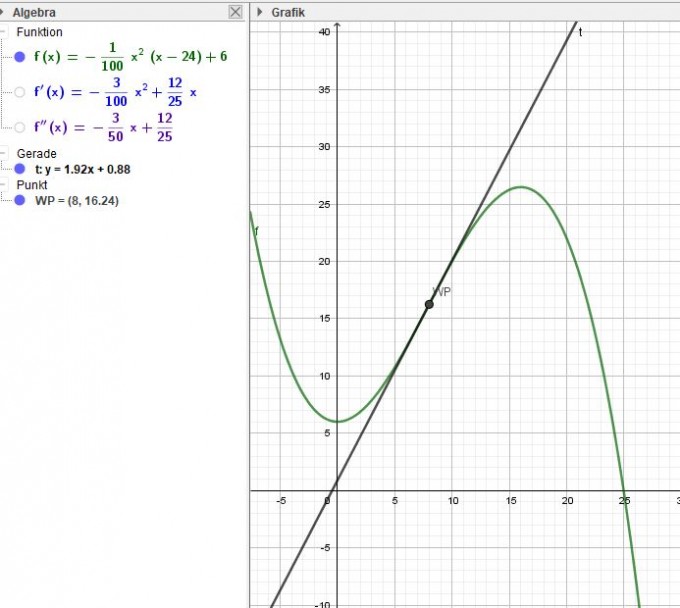
$$f(t) = -\frac{1}{100}t^2\cdot (t-24)+6\\f(t)=-\frac{1}{100}t^3+\frac{6}{25}t^2+6\\f'(t)= -\frac{3}{100}t^2+\frac{12}{25}t\\f''(t)=-\frac{3}{25}t+\frac{12}{25}\\f'''(t)=-\frac{3}{25}\neq 0$$
Um den Wendepunkt zu bestimmen, setzt du die zweite Ableitung = 0 und löst nach t auf. Das Ergebnis setzt du in die Ausgangsgleichung ein, um die y-Koordinate zu bestimmen. (Zur Kontrolle WP (8|16,24).
Die Steigung der Tangente in diesem Punkt erhältst du, indem du 8 für t in die erste Ableitung einsetzt ( = 1,92).
Gruß
Silvia