Wenn man das wie unter https://ourworldindata.org/grapher/future-population-projections-by-country
genauer betrachtet, sind die Kurven komplizierter!
China hat längst gegengesteuert und wächst kaum noch. Indien hingegen wächst weiter (momentan fast linear), so dass bereits 2020 ein Gleichstand erreicht wird:
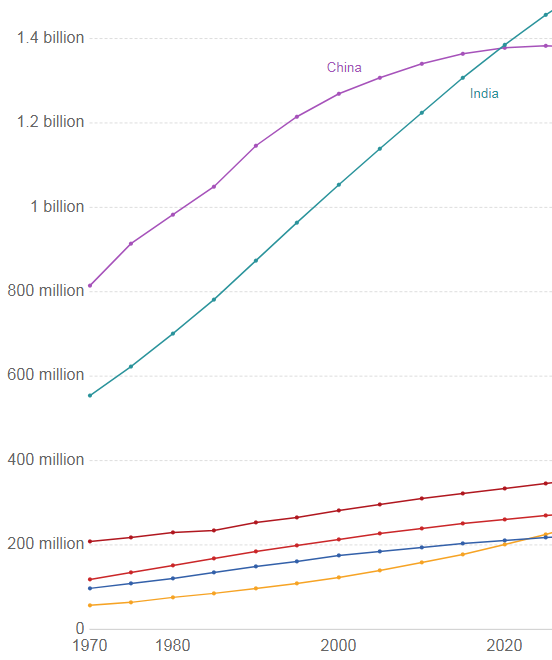
Das zeigt schön, dass man mit zu wenig Quell-Daten (4 Punkten) -> zu ungenaue Prognosen bekommt.
Die primitivste Theorie:
Theorie 1: lineare Funktionen
China:
1993: 1.178mrd
2000: 1.255mrd
f(x)= 0.011*x-20.745
Indien:
1993: 0.898mrd
2000: 1.022mrd
f(x)= 0.017714285714285714*x-34.406571428571425
Gleichsetzung:
0.011*x-20.745=0.017714285714285714*x-34.406571428571425
x=2034.7 nach Christus -> viel zu spät,
da Indien 2000 schon 1.05 Mrd. hatte!
Also bessere Theorie 2:
Indien wächst linear mit besserem Wert 1.025 Mrd. im Jahr 2000:
f(x)= 0.018142857142857127*x-35.26071428571425
China fällt mit fallender Kurve (1-Kind-Politik) -> log-Fallend:
f(x)=0.3408681746*ln(x - 1960.970125)
0.018142857142857127*x-35.26071428571425 = 0.3408681746*log(x - 1960.970125)
Newton-Iteration per Null-Funktion:
0.3408681746*log(x-1960.970125)-0.018142857142857127*x+35.26071428571425
http://www.gerdlamprecht.de/Roemisch_JAVA.htm#0.3408681746*log(x-1960.970125)-0.018142857142857127*x+35.26071428571425@Na=0;@B0]=2010;//Startwert@Nb=@Bi];a=@Bi+1]=b-Fx(b)/@Lb);@N@Aa-b)%3C4e-8@N1@N0@N#
Ergibt
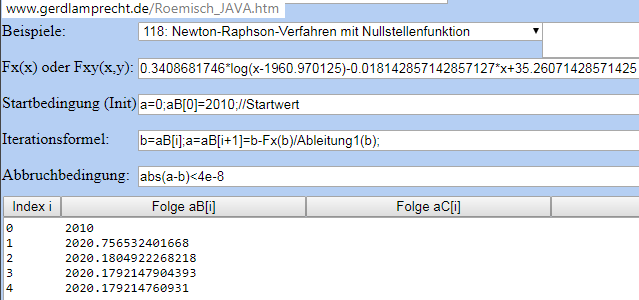
den viel genaueren Wert des Jahres 2020.179...
Und das Diagramm dazu: http://www.gerdlamprecht.de/Liniendiagramm_Scientific_plotter.htm
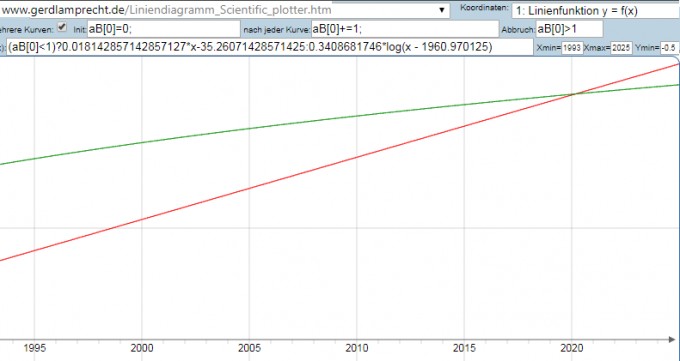
Theorie 3 (Schule): exponentielles Wachstum für beide f(x)=f(0)*e^{k*x}
1993 1.178
2000 1.255
China: f(x)=1.745612755e-8*exp(9.045355337e-3*x) = 1.745612755e-8*e^{9.045355337e-3*x}
Indien:
1993 0.898
2000 1.022
f(x)=9.111226819e-17*exp(1.847810035e-2*x)
Gleichsetzung
1.745612755e-8*exp(9.045355337e-3*x)=9.111226819e-17*exp(1.847810035e-2*x)
e^{0.0184781 x} = 1.91589×10^8 *e^{0.00904536 x} | /e^{0.00904536 x}
e^{0.00943274 x}= 1.91589×10^8 | ln auf beiden Seiten
0.00943274 x = ln(1.91589e8)
x = ln(1.91589e8)/0.00943274
x= 2021.77342