Hinweis:
Betrachte die Menge \(H = \left\lbrace z\in\mathbb{C}\middle| \text{Im}\left(z\right)<\frac{1}{2}\right\rbrace\) und die holomorphe Funktion $$f : H\to \mathbb{C}, \quad z\mapsto \frac{1}{(z-\text{i})\cdot\ldots\cdot(z-n\text{i})}\text{.}$$
Für \(R>0\) betrachte den geschlossenen Weg \(\gamma_R\), der sich aus den Wegen \(\alpha_R : [-R, R]\to H,\quad t\mapsto t\) und \(\beta_R : [0, \pi]\to H, \quad t\mapsto R\cdot \text{e}^{-\text{i}t}\) zusammensetzt.
Betrachte dann das Integral $$\int_{\gamma_R}f\left(z\right)\,\text{d}z\text{.}$$
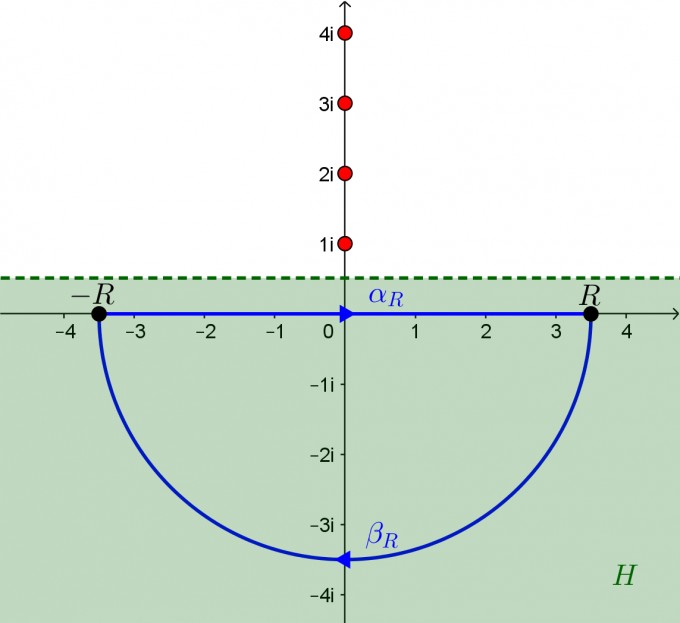
[spoiler]
\(f : H \to \mathbb{C}\) ist eine holomorphe Funktion auf dem einfach-zusammenhängenden Gebiet \(H\). \(\gamma_R\) ist für jedes \(R>0\) ein in \(H\) verlaufender geschlossener Weg. Nach Cauchy-Integralsatz ist $$\int_{\gamma_R}f\left(z\right)\,\text{d}z = 0\text{.}$$
Für jedes \(R > 0\) ist $$\begin{aligned}\int_{\alpha_R}f\left(z\right)\,\text{d}z & = \int_{-R}^{R}f\left(\alpha_R\left(t\right)\right)\cdot\alpha_R'\left(t\right)\,\text{d}t \\ & = \int_{-R}^{R}f\left(t\right)\cdot 1\,\text{d}t \\ & = \int_{-R}^{R}\frac{1}{(t-\text{i})\cdot\ldots\cdot(t-n\text{i})}\,\text{d}t \\ & = \int_{-R}^{R}\frac{1}{(x-\text{i})\cdot\ldots\cdot(x-n\text{i})}\,\text{d}x \\ & \xrightarrow{R\to\infty} \int_{-\infty}^{\infty}\frac{1}{(x-\text{i})\cdot\ldots\cdot(x-n\text{i})}\,\text{d}x\text{.}\end{aligned}$$
Für \(R>n\) ist $$\begin{aligned}\left\lvert\int_{\beta_R}f\left(z\right)\,\text{d}z\right\rvert & = \left\lvert\int_{0}^{\pi} f\left(\beta_R\left(t\right)\right)\cdot \beta_R'\left(t\right)\,\text{d}t\right\rvert \\ & = \left\lvert\int_{0}^{\pi} f\left(\beta_R\left(t\right)\right)\cdot R\cdot \text{e}^{-\text{i}t}\cdot\left(-\text{i}\right)\,\text{d}t\right\rvert \\ & \leq \int_{0}^{\pi}\left\lvert f\left(\beta_R\left(t\right)\right)\cdot R\cdot \text{e}^{-\text{i}t}\cdot\left(-\text{i}\right)\right\rvert\,\text{d}t \\ & = \int_{0}^{\pi}\left\lvert f\left(\beta_R\left(t\right)\right)\right\rvert\cdot R\cdot \underbrace{\left\lvert\text{e}^{-\text{i}t}\right\rvert}_{=1}\cdot\underbrace{\left\lvert -\text{i}\right\rvert}_{=1}\,\text{d}t \\ & = \int_{0}^{\pi}\left\lvert f\left(\beta_R\left(t\right)\right)\right\rvert\cdot R\,\text{d}t \\ & \leq \int_{0}^{\pi}\sup_{\tau\in\left[0, \pi\right]}\left\lvert f\left(\beta_R\left(\tau \right)\right)\right\rvert\cdot R\,\text{d}t \\ & = \sup_{\tau\in\left[0, \pi\right]}\left\lvert f\left(\beta_R\left(\tau \right)\right)\right\rvert\cdot R\cdot \int_{0}^{\pi}\text{d}t \\ & = \sup_{\tau\in\left[0, \pi\right]}\left\lvert f\left(\beta_R\left(\tau \right)\right)\right\rvert\cdot R\cdot \left(\pi - 0\right)\\ & = \sup_{\tau\in\left[0, \pi\right]}\left\lvert f\left(R\cdot \text{e}^{-\text{i}\tau}\right)\right\rvert\cdot R\cdot \pi \\ & = \sup_{\tau\in\left[0, \pi\right]}\left\lvert \frac{1}{(R\cdot \text{e}^{-\text{i}\tau}-\text{i})\cdot\ldots\cdot(R\cdot \text{e}^{-\text{i}\tau}-n\text{i})}\right\rvert\cdot R\cdot \pi \\ & = \sup_{\tau\in\left[0, \pi\right]}\frac{1}{\left\lvert R\cdot \text{e}^{-\text{i}\tau}-\text{i}\right\rvert\cdot\ldots\cdot\left\lvert R\cdot \text{e}^{-\text{i}\tau}-n\text{i}\right\rvert}\cdot R\cdot \pi \\ & \leq \sup_{\tau\in\left[0, \pi\right]}\frac{1}{\left\lvert \left\lvert R\cdot \text{e}^{-\text{i}\tau}\right\rvert-\left\lvert\text{i}\right\rvert\right\rvert\cdot\ldots\cdot\left\lvert \left\lvert R\cdot \text{e}^{-\text{i}\tau}\right\rvert-\left\lvert n\text{i}\right\rvert\right\rvert}\cdot R\cdot \pi \\ & = \sup_{\tau\in\left[0, \pi\right]}\frac{1}{\left\lvert R-1\right\rvert\cdot\ldots\cdot\left\lvert R-n\right\rvert}\cdot R\cdot \pi \\ & = \frac{1}{\left\lvert R-1\right\rvert\cdot\ldots\cdot\left\lvert R-n\right\rvert}\cdot R\cdot \pi \\ & \stackrel{R>n}{=} \frac{1}{\left( R-1\right)\cdot\ldots\cdot\left( R-n\right)}\cdot R\cdot \pi \\ & \stackrel{R>n}{\leq} \frac{1}{\left( R-n\right)\cdot\ldots\cdot\left( R-n\right)}\cdot R\cdot \pi \\ & = \frac{1}{\left( R-n\right)^{n}}\cdot R\cdot \pi \\ & = \frac{1}{\left( 1-\frac{n}{R}\right)^{n}}\cdot R^{1-n}\cdot \pi \\ & \xrightarrow{\begin{matrix}[n\geq 2]\\ R\to\infty\end{matrix}} \frac{1}{\left( 1-0\right)^{n}}\cdot 0\cdot \pi = 0\text{.}\end{aligned}$$
Da sich \(\gamma_R\) aus den Wegen \(\alpha_R\) und \(\beta_R\) zusammensetzt ist $$\int_{\gamma_R}f\left(z\right) = \int_{\\alpha_R}f\left(z\right) + \int_{\beta_R}f\left(z\right),$$ woraus man für \(R\to \infty\) nun $$0 = \int_{-\infty}^{\infty}\frac{1}{(x-\text{i})\cdot\ldots\cdot(x-n\text{i})}\,\text{d}x + 0$$ erhält.
Demnach ist also $$\int_{-\infty}^{\infty}\frac{1}{(x-\text{i})\cdot\ldots\cdot(x-n\text{i})}\,\text{d}x = 0\text{.}$$
[/spoiler]
[spoiler]
An einer Stelle habe ich $$\lim_{R\to\infty}\int_{-R}^{R}\frac{1}{(x-\text{i})\cdot\ldots\cdot(x-n\text{i})}\,\text{d}x = \int_{-\infty}^{\infty}\frac{1}{(x-\text{i})\cdot\ldots\cdot(x-n\text{i})}\,\text{d}x$$ verwendet. Um das machen zu können, muss jedoch das uneigentliche Integral $$\int_{-\infty}^{\infty}\frac{1}{(x-\text{i})\cdot\ldots\cdot(x-n\text{i})}\,\text{d}x$$ existieren. Um die Existenz zu zeigen, kann man das Integral beispielsweise geeignet abschätzen und das Majorantenkriterium verwenden. Das wird gut gehen, da der Integrand eine gebrochen-rationale Funktion ist, bei der der Nennergrad um mindestens 2 größer ist als der Zählergrad.
[/spoiler]