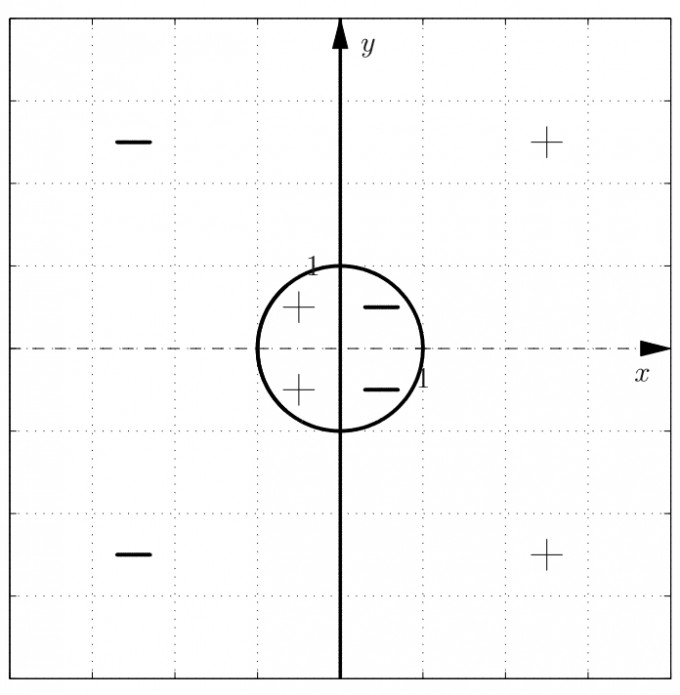
Gegeben sei die Funktion f : ℝ2 → ℝ: (x,y) ↦ x3 + xy2 - x
Skizzieren Sie die Gebiete, für die
f(x,y)=0, f(x,y) > 0, f(x,y) < 0 ist.
Hier seht ihr die Lösung. Auf den Kreis komme ich soweit. Allerdings bin ich irgendwie nicht in der Lage + und - zu bestimmen.