Question

Berechnen Sie die Summen in Abhängigkeit von n

a) summe(i*4^k) von 0 nach n

b) summe((-1/3)^k) von 0 nach n

c) 1-1/3+1/9-1/27+...+1/(-3)^n

Ist meine Lösung mit Hilfe der geometrischen Summe richtig?

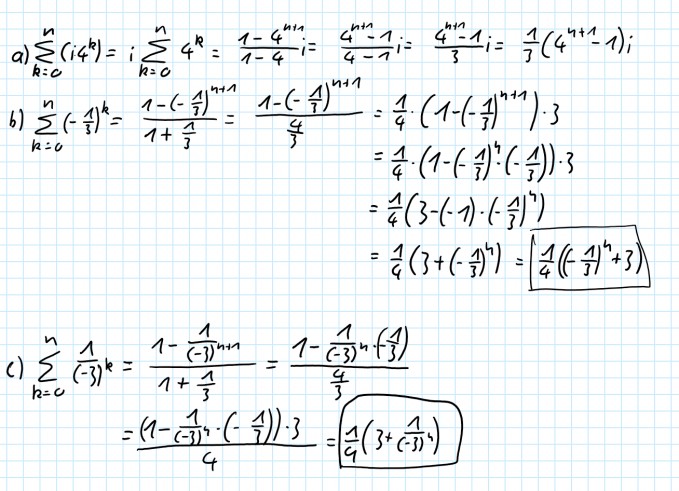
Leider zweifle ich sehr stark an der Richtigkeit, denn setzt man direkt zahlen ein und revhnet nach, kommt man immer auf eine andere Zahl, als würde man direkt ausrechnen.

Habt ihr eine Idee woran es liegen könnte.

Answer 1

Hallo

 bei a kannst du i^k nicht aus der Summe ziehen!  für i^k gibt es 4 Möglichkeiten

 i^1=i , i^2=-1, i^3=-i i^4=1 mit i^5=i fängt es von vorne an!

b und c, dasselbe denn 1/(-3)^k=(-1/3)^k

ist richtig, vielleicht solltest du das Resultat für n gerade und ungerade einzeln aufschreiben.

warum du beim direkt rechnen nich dasselbe rauskriegst weiss ich nicht.

Gruß lul

Comments

bei a) kommt i^k gar nicht vor, sondern i*4^k. Also stimmt die Rechnung.

---

Hallo

danke Hallo , das hatte ich übersehen, wohl wegen der überflüssigen Klammer.

Gruß lul

Answer 2

deine Rechnungen stimmen alle. b) und c) sind gleich, nur halt anders aufgeschrieben. Das kann mit den Potenzgesetzen leicht nachrrechnen.

Falls du dir grundsätzlich unsicher sein solltest, dich verrechnet zu haben, könntest du ja mittels vollständiger Induktion dein Resultat auf die Probe stellen, indem du es einfach beweisen tust.

Comments

danke erstmal für die Hilfe:)

Eine Frage habe ich noch und zwar:

Abgesehen von der VI, kann man es nicht anders nachprüfen?

Wenn ich zB bei der c) k=3 nehme, müsste da nicht für die Gleichung vor und nach der Umformung dad selbe herauskommen?

Wenn nein woran liegt das?

Ich muss gestehen, dass ich dies hier einfach mechanisch runtergerechnet habe ohne es groß verstanden zu haben.

---

Hat sich erledigt, rechnen muss man können xd

---

du kannst dir ja auch die Herleitung für die geometrische Summenformel angucken. Das hat mir persönlich sehr geholfen und erstrecht dafür, diese Formel zu verinnerlichen.